TIPS AND TRICKS - SISTEMI DIGITALI
Buona parte delle soluzioni si basano sull’esame del 01/06/2018
Sistemi Digitali
Conversioni varie
Base 10 → Base qualsiasi:
- dividere il numero per “base qualsiasi” fino a quando il quoziente non sarà 0
- segnarsi i resti e prenderli dall’ultimo al primo
Es. 329 in base 10 scriverlo in base 4:
329 / 4 = 82 resto 1
82 / 4 = 20 resto 2
20 / 4 = 5 resto 0
5 / 4 = 1 resto 1
1 / 4 = 0 resto 1
Quindi il numero 329 risulterà essere 11021 in base 4
Base qualsiasi → base 10:
- prendere ogni cifra del numero di partenza a partire dall’ultima e andare via via verso la prima, e applicare questa semplice formula:
cifra del numero * “base di partenza” ^ n_posto (partendo da 0) - nell’esempio di prima verifichiamo la correttezza del numero trasformandolo in decimale:
11021 scorro dall’ultima alla penultima quindi 1 2 0 1 1
Il numero in decimale sarà uguale a:
1 * 4^0 = 1 +
2 * 4^1 = 8 +
0 * 4^2 = 0 +
1 * 4^3 = 64 +
1 * 4^4 = 256 =
329
Base “esponente di 2” → 2:
Esprimere ogni cifra del numero in base 2 utilizzando n bit (dove n sarebbe il numero di volte per il quale 2 è elevato per raggiungere la cifra dell’esponente).
Esempio:
F4A da base 16 a base 2 è 1111 0100 1010
Infatti per esprimere ogni cifra in base 16 ho usato 4 bit perchè 16 è 2
Complemento a 2
Un modo per rappresentare i numeri binari è quello di utilizzare il complemento a 2.
Normalmente avendo assegnati tot bit, sarà sufficiente aggiungere degli 0 davanti al numero per farlo diventare di tot bit.
Es. 1010 avendo a disposizione 8 bit, diventerà: 0000 1010
Il complemento a 2 serve per rappresentare un numero negativo.
Per ottenerlo bisogna:
- invertire tutte le sue cifre
- sommare 1
Es. 0000 1010 (10 in decimale) in ca2 sarà 1111 0101 + 1 = 1111 0110 (-10).
Per verificare la correttezza dei calcoli basterà effettuare una normale conversione da binario a decimale, con l’accortezza di far assumere al numero in testa il valore negativo.
Es. 2 + 4 + 16 + 32 + 64 -128 = -10
Operazioni con i numeri non in base 10
Le operazioni sono come in base 10, solo che anziché avere un riporto quando si arriva a 10 lo si ha quando si arriva a “base”.
Nota importante per i numeri binari: la moltiplicazione ha SEMPRE il doppio del numero di bit del numero più grande. Se ad esempio si moltiplicano due numeri, il primo di 5 cifre, il secondo di 3, la moltiplicazione avrà grandezza 10 bit.
Operazioni con i numeri binari
Il procedimento consigliato per tutti gli esercizi è:
- avere A e B positivi, aggiungendo eventuali zeri per portarli in CA2
- fare il CA2 di A e B in modo da trovare questi numeri negativi
- effettuare qualunque operazione come una normale addizione
Es. avendo 8 bit a disposizione eseguire a+b e a-b
A = 1010010
B = 110
- porto ad avere i due numeri a 8 bit:
A = 01010010
B = 00000110 - calcolo -A e -B facendo il CA2:
-A = 10101110
-B = 11111010
A + B = 01010010 + 00000110 = 01011000
A - B = 0 1 0 1 0 0 1 0 +
1 1 1 1 1 0 1 0 =
0 1 0 0 1 1 0 0
Progettazione automi
In questo esercizio viene proposto, date delle specifiche, di progettare un automa, eventualmente minimizzandolo.
Testo dell’esercizio
Progettare un automa che riceve in ingresso i simboli 0 e 1 e dà in output 1 ogni volta che gli ultimi 3 bit ricevuti (anche con sovrapposizioni) rappresentano un numero intero in Ca2 che divide 9. Si ignorino i primi due output restituiti (nel senso che possono assumere qualsiasi valore).
input: 00101100
output: 00101100
Svolgimento
Ci sono due approcci per risolvere questo esercizio, entrambe hanno la stessa soluzione (solo che richiedono più passaggi).
Il primo è considerare 3 bit dell’output, il secondo è considerare solo 2 bit dell’output perchè il terzo è dato dall’input.
L’esercizio verrà svolto utilizzando il secondo approccio, poichè più semplice e veloce, tuttavia verrà aperta una piccola parentesi sul primo.
- Si disegna l’automa: siccome gli stati di input sono trascurabili possiamo tranquillamente ignorarli e iniziare da 00.
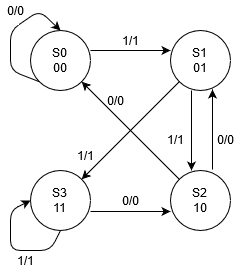
Perchè da 00?
Potevamo iniziare da qualsiasi stato, è stato scelto 00 per comodità.
Sempre per comodità, siccome il terzo bit è quello determinante per gli stati dell’automa, si è deciso di non complicare ulteriormente la situazione prendendo in considerazione effettivamente 2+1 bit: i 2 bit rappresentano lo stato, il terzo è l’input che diventerà man mano il nome degli altri stati.
Per disegnare l’automa bisogna ragionare un attimo sulle sue specifiche. In questo caso è stato richiesto di produrre un determinato output a fronte di un particolare input.
Si disegna quindi una freccia da ogni stato a seguito di ogni input indicando su ogni freccia input e output prodotti.
Nel problema in questo caso è richiesto che l’automa produca 1 come risultato nel caso il numero rappresentato in ca2 divida il numero 9.
I numeri che dividono 3 sono:
- 1: 001, 111
- 3: 101, 011
Vanno considerati anche i casi -3 e -1, poiché si tratta di rappresentazioni in ca2.
Se si hanno ancora dubbi andare a vedere la sequenza di output e analizzarli a 3 bit alla volta.
Esistono due rappresentazioni:
- Mealy
- Moore
Sono perfettamente equivalenti ed intercambiabili, tuttavia quella maggiormente e tipicamente utilizzata è quella di Mealy, utilizzata in questo caso.
Rappresentazione dell’automa in forma tabellare:
In questa rappresentazione, l’automa viene descritto sotto forma di tabella a doppia entrata, avente come variabili gli stati e gli input.
Le varie celle andranno riempite con <stato destinazione dato quel determinato input> / <output con quel determinato input>
| 0 | 1 | |
|---|---|---|
| S0 / 00 | S0 / 0 | S1 / 1 |
| S1 / 01 | S2 / 0 | S3 / 1 |
| S2 / 10 | S0 / 0 | S1 / 1 |
| S3 / 11 | S2 / 0 | S3 / 1 |
Tutte queste informazioni si apprendono dal disegno:
- S0: va su se stesso con input 0 (siamo nella colonna dello 0) e dà 0 come output;
va in S1 con input 1 (colonna dell’1) e dà 1 come output.
- S1: va in S2 con input 0 e dà 0 come output;
va in S3 con input 1 e dà 1 come output
…
Tabella triangolare
Bisognerà procedere alla stesura della tabella triangolare.
Questa tabella serve per minimizzare l’automa, cioè per renderlo più semplice rispetto all’automa inizialmente creato e analizzato.
La tabella deve essere composta: a sinistra tutti gli stati meno il primo
In basso tutti gli stati meno l’ultimo
Infatti, basterà analizzare le coppie di stati singolarmente, non serve “duplicare la tabella”.
In questo caso:
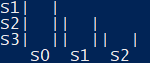
Definizione:
- una coppia di stati si dice fondibile quando a seguito dello stesso input ha output uguali e stati di destinazione uguali
- quando una coppia di stati ha output diversi a fronte dello stesso input si mette una X
La X indica una coppia di stati che non può essere fusa.
Rappr. Tabellare:
| 0 | 1 | |
|---|---|---|
| S0 / 00 | S0 / 0 | S1 / 1 |
| S1 / 01 | S2 / 0 | S3 / 1 |
| S2 / 10 | S0 / 0 | S1 / 1 |
| S3 / 11 | S2 / 0 | S3 / 1 |
La tabella si riempie seguendo questi step facendo riferimento alla rappresentazione tabellare:
- mettere una X dove la coppia ha gli output diversi a fronte dello stesso input.
In questo particolare esempio si può vedere che tutte le coppie hanno output identico, e quindi si lasciano le celle in bianco
Es. 0 e 1 hanno sia con 0 che con 1 output 0 e 1 rispettivamente (vedere la parte dopo lo slash nella rappresentazione tabellare). Di conseguenza è impossibile
- analizzare le dipendenze delle varie coppie → bisogna vedere le dipendenze di ogni coppia di stati.
Ad esempio:
Nella coppia 0 1 si va a vedere (prima in riga e poi in colonna) da chi dipendono, cioè la parte prima dello slash.
In questo caso
| S0 / 0 | S1 / 1 |
|---|---|
| S2 / 0 | S3 / 1 |
Quindi la coppia 0 1 dipende dalla coppia 0 1 e 2 3.
Siccome però 0 1 sarebbe la coppia stessa, si prende in considerazione solo l’altra
coppia, 2 3 e si va a riportare questo dato nella tabella
Coppia 0 2: stessi stati.
Si mette un O nella tabella
Coppia 0 3: stesso discorso della 0 1
| S0 / 0 | S1 / 1 |
|---|---|
| S2 / 0 | S3 / 1 |
ma in questo caso, procediamo per colonna (siccome non c’è lo stato stesso in riga).
La dipendenza risulterà essere 0 2 e 1 3
…
- Alla fine dello step precedente la tabella risulterà essere:
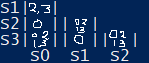
Si nota una cosa molto importante: la coppia 1 3 ha un O.
Si cancellano da tutte le altre caselle la coppia 1 3

Stesso discorso per 0 2:
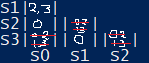
Ora le celle sono vuote perché tutti gli elementi dipendenti sono stati cancellati:
si rimpiazzano queste celle con dei cerchi.
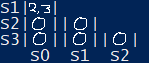
Stessa cosa con 2 3.
La tabella risulterà essere alla fine:
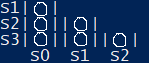
- Si passa alla fusione degli stati: si prende la coppia con il cerchio, si prende uno dei due estremi e il nuovo stato avrà le caratteristiche che avevano i due stati originali.
In questo caso: si ha un solo stato poiché tutti gli stati sono fondibili tra di loro.
OPZIONALE: si ridisegna il nuovo automa e si crea una nuova tabella
Verificare espressione booleana
Questo esercizio nonostante possa sembrare complicato, in realtà è il più semplice.
Bisogna sviluppare le varie espressioni dall’espressione più lunga e complicata e rendere il tutto “semplificabile” fino a trovare un’espressione più semplice.
Le leggi si riassumono in:


Oltre a questo:
- consenso: xy + x’z + yz = xy + x’z
- DeMorgan: “negazione generale”: cambi i + in * e viceversa
Neghi ciò che affermi e affermi ciò che neghi
(es. (a’+b)’ = ab’) - xor: a xor b = a’b + ab’
Ogni volta che si va a verificare un’espressione booleana:
- svolgere tutti i prodotti
- svolgere DeMorgan
- semplificare con i teoremi in modo tale da ritrovarsi l’espressione a destra / sinistra dell’uguale
Es.
(z’(x+y))’ + (y xor z)’ = y’ + z
(xz’ + yz’)’ + (yz’ + y’z)’ sviluppo prodotti
(x’ + z) * (y’ + z) + (y’ + z)(y + z’) DeMorgan
x’y’ + x’z + y’z + z + y’z’ + yz sviluppo prodotti
A questo punto posso semplificare:
x’y’ + y’z + z raccolgo z e tolgo yz, y’z e x’z
y’z + z consenso
L’espressione trovata coincide con l’espressione a destra dell’uguale.
Interconnessioni tra registri
Ossia, collegare i registri tra di loro “come se fosse un programma”.
Regole (per fare qualcosa)
- maggiore tra 2 registri: utilizzare un cmp (ha due uscite, una restituisce >=)
- minore tra 2 registri: utilizzare un cmp (ha due uscite, metterle in xor)
- somma registri pari o dispari: utilizzare adder e prendere l’lsb della somma. Metterla in AND con 1 per vedere se è dispari, in OR con 0 se è pari
- sottrazione registri: come la somma ma al secondo operando va aggiunto il not prima di farlo entrare nell’adder
- qualcosa positivo o negativo: msb e AND con 1 per vedere se è negativo, OR con 0 per vedere se è negativo
- gestire l’altrimenti: tipicamente è associato un mux (se la somma è … fai questo altrimenti fai quell’altro). L’uscita dell’adder si mette come bit di controllo al mux.
- “la scrittura dei registri è abilitata se…” collegare il pezzo sviluppato dopo il se con ogni registro
Traccia
Siano S0, S1 e S2 tre registri sorgente e D0, D1, D2e D3 quattro registri destinazione.
Si progetti la rete di interconnessione tale che:
- in D0 viene trasferito S0 se il contenuto di S2 è pari, la somma aritmetica tra S1 e S2 altrimenti
- S1 viene trasferito in D1 se la somma aritmetica tra S0 e S1 è negativa
- S2 viene trasferito in D2 se D1 > D2, altrimenti viene trasferito in D3.
- Tutti i trasferimenti sono abilitati se il contenuto di S0 è divisibile per 4
Svolgimento
- collegare ai registri destinazioni i “mini-circuitini” dei registri sorgenti.
Vedere le regole per capire come connettere i registri tra di loro e rispettare la traccia.
Analisi di un circuito
Dato un circuito analizzalo tirando fuori tutto ciò che puoi tirare fuori a seconda di che ti chiede il problema. Potrebbe essere qualcosa tra le seguenti cose: SOP, POS, MIN-POS, MIN-SOP, FCD e FCC, FORMA NORMALE, ROM, PLA, MUX, DUALE, COMPLEMENTARE, ALL-NAND, ALL-NOR, TV (tavola verità)
Testo dell’esercizio:

Svolgimento:
Operazioni e conversioni numeri con segno, mantissa, esponente
Rappresentazione in <s, m, e>
Testo dell’esercizio:
Dati X=<0;10010100;1101> e Y=<1;11010100;1100> si esegua la somma X+Y e si rappresenti il risultato con 8 bit di mantissa e 4 di esponente come gli operandi.
Svolgimento:
Analisi di un circuito RC
Rappresentazione in <s, m, e>
Testo dell’esercizio:
Si disegni il diagramma temporale del seguente circuito per 4 colpi di clock, supponendo che inizialmente tutti i FF (quelli del CNT e quello esterno) assumano valore 0:
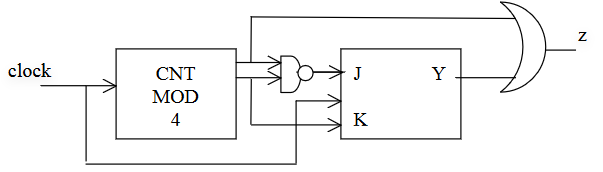
Si proceda poi all’analisi del circuito fino all’automa associato.
Svolgimento: