aa. 2021-2022: si ringraziano gli studenti R. B. e I. S. per le correzioni e revisioni, M. A. per le immagini degli esercizi LR(0), P. per l’immagine di Erschev.

Linguaggi e Compilatori

ER: costruire NFA a partire da un’espressione regolare

Ci sono due passi fondamentali:

1. Costruire l’albero astratto. Per farlo basta “risolvere” l’espressione regolare in maniera “spezzettata”, a blocchi di parentesi.
2. Disegnare l’automa NFA a pezzi

Testo d’esempio

L’espressione è la seguente:

(a|c)*(c|b)*(abc)*

Regole per fare l’albero astratto

Regole da tenere ben presente:

1. L’associatività a sinistra

2. OR (a|c):

     |
    / \
   a   b
   

3. AND (abc)*:

       *
       |
       °
      / \
     °   c
    / \
   a   b
   

Passo 1: l’albero astratto

            °
           /  \
          /    \
         /      \
        /        \
       /          \
      °            *
     / \            \
    /   \            °
   *     *          / \
   |     |         /   \
  / \   / \       °     c
 a   c c   b     / \
                a   b

Passo 2: l’automa

Mi disegno i vari automi e li unisco tra loro.

Regole per disegnare l’automa

• Disegno prima gli automi semplici (atomici, esempio, automa che riconosce a, automa che riconosce c) e li unisco
  • Sebbene possa aver disegnato già un altro automa in precedenza che facesse la stessa cosa, per ogni ramo devo disegnare un automa diverso
    Esempio: se ho già disegnato un automa che riconosce a e mi ritrovo a dover disegnare un ramo con un automa che riconosce a devo disegnarlo di nuovo
• Concatenazione (or)
  • aggiungo uno stato vuoto iniziale
  • faccio due branch con gli automi creati in precedenza
  • aggiungo uno stato vuoto alla fine
  • i due stati supplementari avranno epsilon nelle frecce
• Unione (and)
  • prendo i due sottoautomi e li unisco tra loro andando a creare un nuovo stato
  • quest ultimo avrà come nome “stato finale sottoautoma1 / stato iniziale sottoautoma2”
• Kleine (*)
  • come concatenazione (stati supplementari) ma al primo fai una freccia che va all’ultimo e il penultimo va nel secondo. Ovviamente entrambe le frecce hanno epsilon.

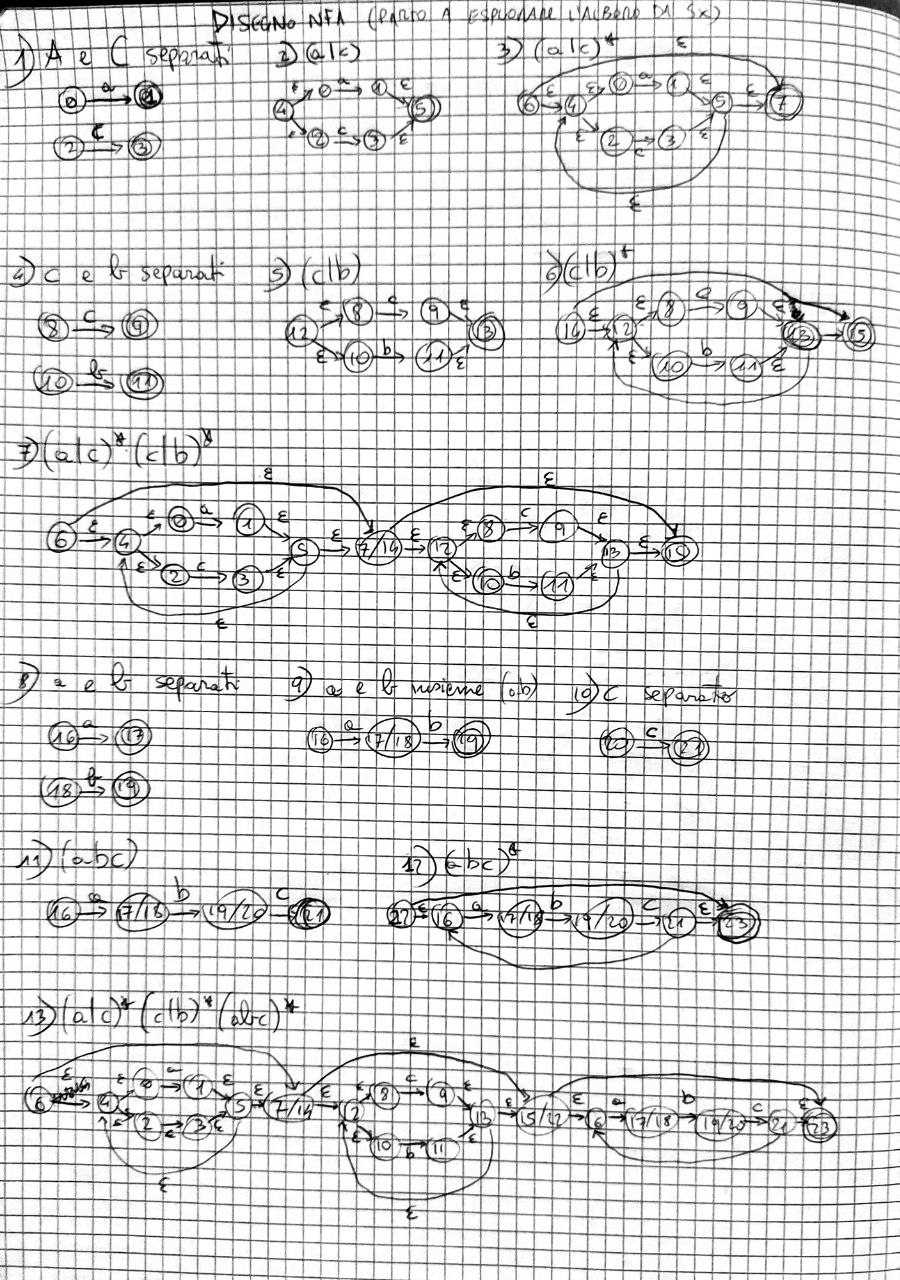
Disegno dell’automa

Guardando l’albero astratto, parti dall’estrema sinistra e cominci a fare piccoli sottoautomi. Man mano che risali l’albero unisci a seconda di quello che trovi.

NFA: usare subset construction per costruire un DFA partendo da un NFA

Traccia

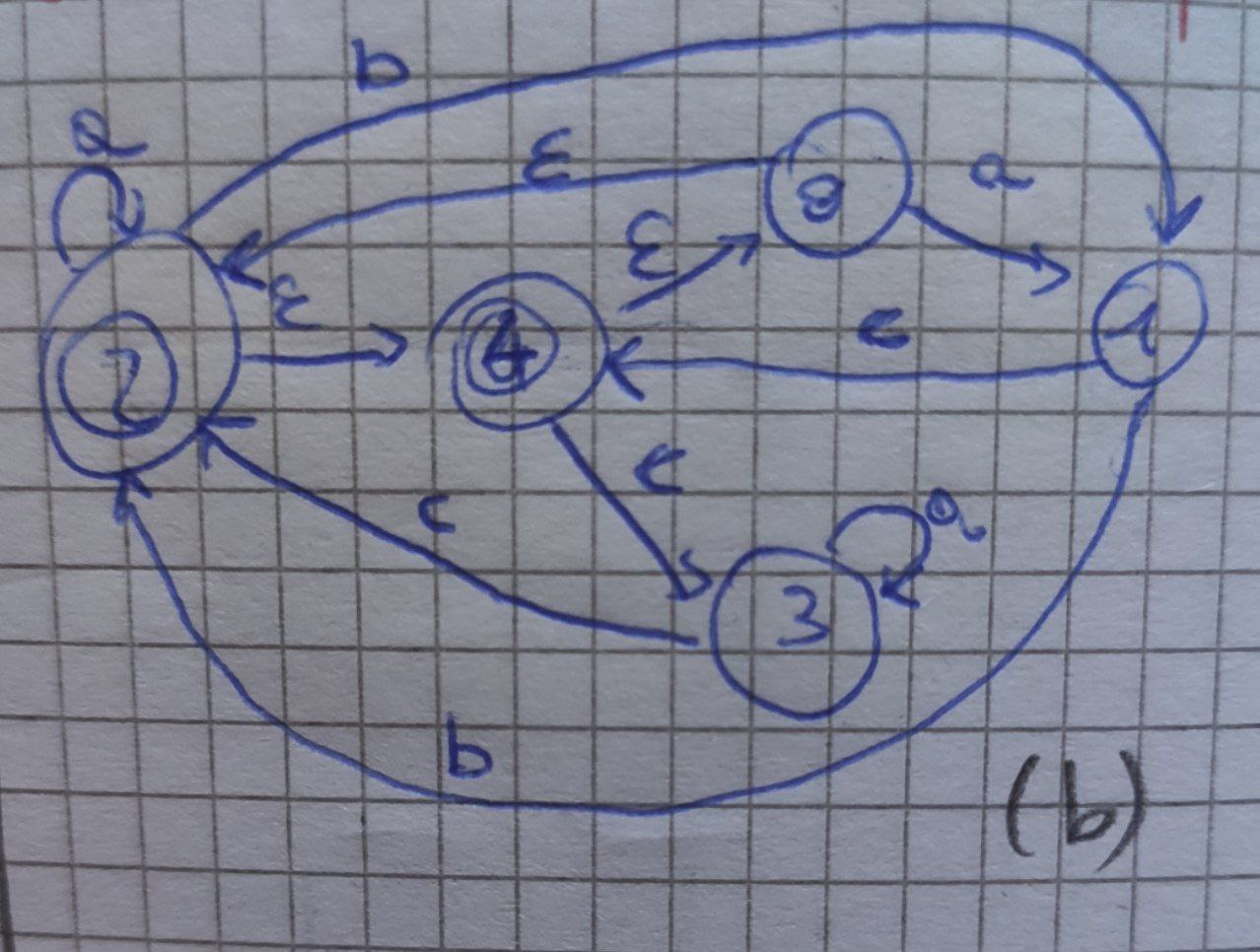
Cosa bisogna fare

1. Si sceglie uno stato iniziale, 0 nel nostro caso, e si calcola la sua ε-closure ossia seguendo le frecce con la ε, bisogna vedere dove si finisce. Questo andrà a formare il nostro stato di partenza. Nel nostro caso: {0,2,4) = A.
2. Si calcola la move per lo stato A: per ogni stato in A vedo dove vanno gli stati con tutti gli input dell’automa, quindi, prima con a, poi con b e poi con c. Devo inoltre calcolare ogni volta la ε-closure. Ogni volta che trovo un nuovo gruppo “che non ho mai visto” creo un nuovo stato. Esempio: se calcolo la move di A, il gruppo di prima, con l’input a, ottengo ε-closure({1,2}) = {0,1,2,4}. Siccome non ho mai visto in precedenza questa partizione, posso chiamarla B. In seguito, calcolerò anche le sue move.
3. Continuo finché non trovo altri stati

Calcoli e procedimento

Promemoria efficaci:

• dopo il secondo uguale, devo SEMPRE riscrivere gli stati che avevo scritto dopo il primo uguale
• lo stato vuoto è uno stato come tutti gli altri. In quanto tale ha un nome. Alla fine, verrà rappresentato come uno stato che non ha frecce entranti verso gli altri stati, e ogni input andrà in sé stesso.
• se non finisco da nessuna parte, scriverò ∅

1. Stato in D: ε-closure(0) = {0,2,4} (A)
2. ε**-**closure(move(A, a)) = ε-closure({1,2}) = {0,1,2,4} (B) ⇐ dopo il primo uguale: “dove vado con input a da 0,2,4 (A)?“. Dopo il secondo uguale: “dove vado con ε da 1 e 2?”.
3. ε**-**closure(move(A, b)) = ε-closure({1}) = {1} (C)
4. ε**-**closure(move(A, c)) = ε-closure({3}) = {3} (D)
   Bene, ora ho come nuovi stati B, C e D. Devo continuare.
5. ε**-**closure(move(B, a)) = ε-closure({1, 2}) = (B) ⇐ me l’ero già calcolato al passo 2
6. ε**-**closure(move(B, b)) = ε-closure({1, 2}) = (B)
7. ε**-**closure(move(B, c)) = ε-closure({3, 4}) = {0,2,3,4} (E)
8. ε**-**closure(move(C, a)) = ε-closure({∅}) = {∅} (G)
9. ε**-**closure(move(C, b)) = ε-closure({2}) = {0,2,4} (A)
10. ε**-**closure(move(C, c)) = ε-closure({4}) = {0,2,4} (A)
11. ε**-**closure(move(D, a)) = ε-closure({3}) = (D)
12. ε**-**closure(move(D, b)) = ε-closure({∅}) = {∅} (G)
13. ε**-**closure(move(D, c)) = ε-closure({2}) = (A)
14. ε**-**closure(move(E, a)) = ε-closure({1, 2, 3}) = {0, 1, 2, 3, 4} (F)
15. ε**-**closure(move(E, b)) = ε-closure({1}) = (C)
16. ε**-**closure(move(E, c)) = ε-closure({2, 3}) = {0, 2, 3, 4} (E)
17. ε**-**closure(move(F, a)) = ε-closure({1, 2, 3}) = (F)
18. ε**-**closure(move(F, b)) = ε-closure({1, 2}) = (B)
19. ε**-**closure(move(F, c)) = ε-closure({2, 3, 4}) = (E)
20. G è uno stato vuoto. Siccome, tra le altre cose non ha archi uscenti, posso non rappresentarlo.

Va bene, e adesso? Il DFA

Gli stati finali del DFA sono tutti quelli in cui, nel lavoro fatto in precedenza compare almeno uno stato finale dell’NFA.

Ad esempio, E contiene 2 e 4, dunque è sicuramente uno stato finale.

Nell’NFA gli stati finali erano 2 e 4.

Posso quindi disegnare l’automa (va bene anche la forma tabellare, in grassetto gli stati finali):

stato / input	a	b	c
A	B	C	D
B	B	B	E
C	G	A	A
D	D	G	A
E	F	C	E
F	F	B	E
G	G	G	G

MIN: minimizzare gli stati di un DFA

Traccia

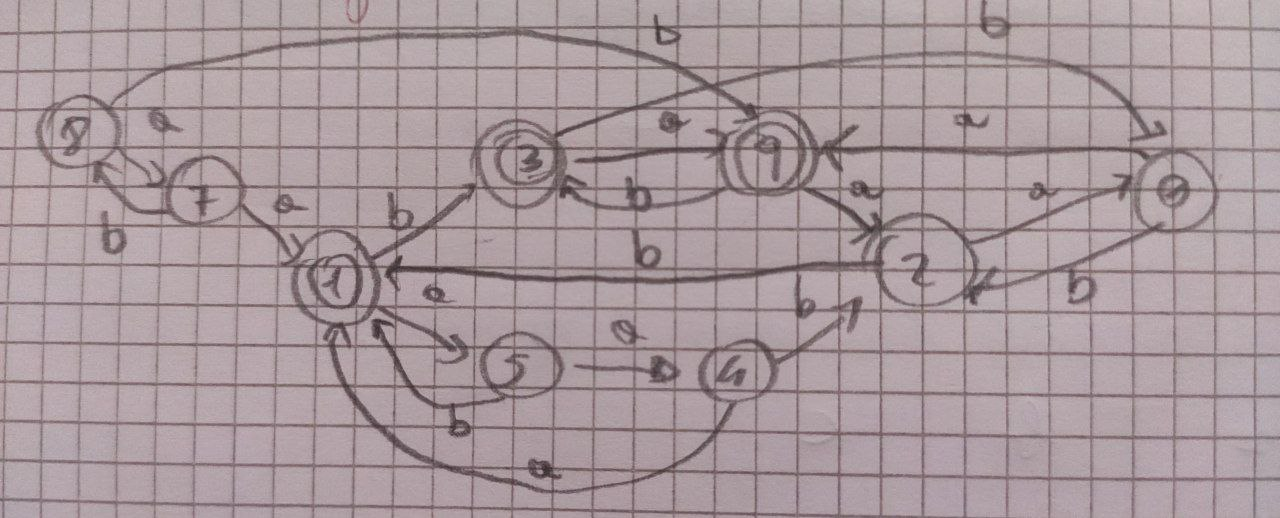
Risoluzione

1. Scrivere fisso le seguenti cose:
   1. sia Π partizione iniziale
   2. sia Πnew partizione di lavoro
   3. sia Πf DFA minimizzato
   4. Σ = {a,b} ⇐ in questo caso a e b perché i simboli usati nell’automa sono solo questi due
   5. Π = {{1,3,9}, {0,2,4,5,7,8}} ⇐ rispettivamente gli stati finali e i restanti
2. Analizza le partizioni che hai creato. Se le dividi, analizza prima quelle divise. Ogni volta che dividi dai un numero a quella partizione, sarà più comodo per altri calcoli che verranno fatti dopo. Costruisci la solita tabella “stato/input”, avendo cura di segnare non tanto lo stato di destinazione, ma la partizione in cui si trova lo stato di destinazione.\

{1, 3, 9} (1), {0,2,4,5,7,8} (2) ⇐ tra parentesi tonde il “nome della partizione”\

stato / input	a	b
1	5 (2)	3 (1)
3	9 (2)	0 (2)
9	2 (2)	3 (1)

Gli stati 1 e 9, a fronte dello stesso input vanno nella stessa partizione di output. Possono rimanere insieme, ma lo stato 3 se ne va per conto suo.\
**Πnew = {1, 9}(1) {3}(3) {2, 5, 8, 0, 4, 7} (2)**\
\
Il 3 non ha discrepanze e quindi non verrà più analizzato. (quando ho un singleton non lo considero).

3. Analizzo la nuova partizione {1, 9}

stato / input	a	b
1	5 (2)	3 (3)
9	2 (2)	3 (3)

Tutto ok. Non posso fondere più di così.

4. Analizzo la partizione 2

stato / input	a	b
0	9 (1)	2 (2)
2	0 (2)	1 (1)
4	1 (1)	2 (2)
5	4 (2)	1 (1)
7	1 (1)	8 (2)
8	7 (2)	9 (1)

Posso quindi staccare sia 0 4 7 che 2 5 8, sempre per il solito motivo che a fronte dello stesso input vanno nelle stesse partizioni di destinazione.\
\
**Πnew = {1, 9}(1) {3}(3) {2, 5, 8} (2) {0, 4, 7}(4)**\\

***

5. Analizzo le partizioni rimanenti. Sono irriducibili.

	a	b
0	9 (1)	2 (2)
4	1 (1)	8 (2)
7	1 (1)	8 (2)

	a	b
2	0 (4)	1 (1)
5	4 (4)	1 (1)
8	7 (4)	9 (1)

Importantissimo: pure se sono irriducibili devi comunque fare il giro “a vuoto”. Finisci SOLO quando non cambi più nulla.

FAT: fattorizzare una grammatica

L’idea

Ricordate i monomi e i polinomi fatti a scuola? Ecco, fattorizzare una grammatica vuol dire fare circa la stessa cosa: trovate i monomi simili, fate raccoglimento e con un po’ di accortezze avrete fattorizzato una grammatica.

Traccia

A → AaBc | AabCa | AaCbA | AaBC | AabCB | AaCbB | AaBa | C
B → BBCB | BcC | BcaA | BCb | BBa | BcaC | C
C → CcBc | CAb | Cc | CCBb | CCC | CAB | CcAa | c

Svolgimento

Identifico i monomi e me li segno in qualche modo nella traccia.

Considero A:

• π = AaB, AabC, AaCb ⇐ ossia, tutte le parti in comune colorate che ho preso in considerazione quando ho raggruppato i monomi simili
• A ⇒ AaBA’ | AabCA” | AaCbA''' | C ⇐ prendo le parti “in comune” e per ogni gruppo ci aggiungo un A’ poi A” ecc. Se un monomio sta per conto suo, bisogna metterlo qui.
  • le clausole con ’, ” ecc conterranno i “pezzi diversi non in comune” con i monomi raggruppati prima. Esempio: AaBc e AaBC in comune hanno AaB. Le loro parti non in comune sono c e C, che sono quelle che andranno a finire nella prima clausola.
• A’ ⇒ c | C | a
• A” ⇒ a | B
• A''' ⇒ A | B

Considero B:

• π = B
• B ⇒ BB’ | C
• B’ ⇒ BCB | cC | caA | Cb | Ba | caC

Considero C:

• π = Cc, CA, CC
• C ⇒ CcC’ | CAC” | CCC''' | c
• C’ ⇒ BC | Aa | ε
• C” ⇒ b | B
• C''' ⇒ Bb | C

RIC: eliminare la ricorsione sinistra da una grammatica

Regolette

SEGUIRE IL SACROSANTO ORDINE

1. PRIMA sostituisco, se c’è qualcosa da sostituire: il concetto dei pronomi. Ad esempio ho A → xA | Bc e B → Az | Cy, dovrò dunque modificare B → Az, e quindi avrò B → xAz | Bcz | Cy
2. POI elimino eventuali ricorsioni
   1. nell’esempio di prima: voglio eliminare la ricorsione B → Bcz
   2. Divido B in due: B → xAzB’ | CyB’ e poi B’ → czB’ | ε
   3. Il primo pezzo si ottiene riscrivendo B di prima, tranne quella che voglio eliminare e ad ogni produzione gli aggiungo B’
   4. Il secondo pezzo si ottiene scrivendo la parte destra della ricorsiva che volevo togliere, tolgo la B, aggiungo la B’ alla fine ed ε
   5. NB: Se dovessi avere dopo la sostituzione, roba che è ancora sostituibile devo sostituire. Esempio: se sostituisco B → Ab | c, e A me l’ero già calcolato, devo sostituirlo.
3. Non ritorno mai su una cosa che avevo già analizzato. Il procedimento è lineare, e una volta che ho finito con A, basta, non posso più modificarlo.

Traccia

A → xA | By
B → Cy | Bw | Az
C → Aw | Bz | Cz | x

Svolgimento

1. Guardo la prima riga. Analizzo A: non ci sono operazioni da effettuare. Non succede nulla. Non ci sono ricorsioni dirette e non possiamo sostituire alcunché. Infatti A → By, potremmo sostituire B, ma non possiamo farlo adesso perché B non lo abbiamo ancora analizzato.
   
   Scrivo:
   > Analizzo A: non ci sono operazioni da effettuare
2. Analizzo B: notiamo che B → Az può essere riscritta: dobbiamo sostituire alla A, la parte destra della produzione di A (che sarebbe xA | By) seguita da z, poiché c’è Az.
   
   Applico la regola 1 → riscrivo pari pari la produzione di B:
   B → Cy | Bw | xA
   e aggiungo z
   B → Cy | Bw | xAz | Byz
   
   Applico adesso la regoletta 2 → tolgo le ricorrenze immediate: B → Bw e B → Byz.
   Riscrivo B con tutte le produzioni meno quelle che voglio togliere:
   B → CyB’ | xAzB’
   poi, prendo le parti che mi interessano e ci aggiungo B’ + simbolo di vuoto come produzione finale:
   B’ → wB’ | yzB’ | e
3. Riscrivo la grammatica aggiornata:
   A → xA | By
   B → CyB’ | xAzB’
   B’ → wB’ | yzB’ | e
   C → Aw | Bz | Cz | x
4. Ho finito con B, ora vado su C.
   Analizzo C: notiamo che C → Aw e C → Bz possono essere riscritti
   
   C → xAw | Byw | CyB’z | xAzB’z | Cz | x
   
   Finito il passo 1? No. Possiamo continuare a sostituire!
   
   C → xAw | CyB’yw | xAzB’yw | CyB’z | xAzB’z | Cz | x
   
   Finito il passo 1? Sì.
   
   Posso togliere le ricorrenze immediate: C → CyB’yw, C → CyB’z, C → Cz
   
   Solita cosa: riscrivo tutto C.
   C → xAwC’ | xAzB’ywC’ | xAzB’zC’ | xC’
   C’ → yB’ywC’ | yB’zC’ | zC’ | e
5. Grammatica finale:
   A → xA | By
   B → CyB’ | xAzB’
   B’ → wB’ | yzB’ | e
   C → xAwC’ | xAzB’ywC’ | xAzB’zC’ | xC’
   C’ → yB’ywC’ | yB’zC’ | zC’ | e\

FF: First e follow

First: TODO

Follow

Devo avere ben presente questa tabella:

A seconda della follow che sto facendo, mi vado a vedere dove sta la lettera della follow (in quale “monomio”).

Siccome si chiama follow, devo vedere in che forma sta tramite la tabella, e regolarmi di conseguenza.

follow(C): dove compare C? bBCe → aggiungo e, primo caso ecc\

BU: LR(0)

Traccia

• S’ → S
• S → AB | aA
• A → bB | cAb | a
• B → Bb | BA | b

Regolette

• Prima sposto il pallino di una posizione a destra, poi calcolo la chiusura
• la chiusura si calcola mettendo l’insieme stesso + tutte le produzioni che hanno a sinistra, il primo simbolo dopo il pallino dell’insieme originale.
• anche per un discorso di coerenza: quando mi ritrovo in una situazione tipo:
  (I0,A) = {S’→A•B} = clos({S’→A•B}) = {S’→A•B, DEVO AGGIUNGERE ANCHE LA ROBA DI B.}
  In caso la roba di B abbiamo altra roba che va in altre lettere (ad esempio se ho aggiunto B → •Cx, DEVO AGGIUNGERE ANCHE LA ROBA DI C).

Svolgimento

Inizialmente costruiamo I (é una I di Imola).

Questo insieme si costruisce in questo modo: partiamo da S’. Da S’ vado a S, quindi sicuramente metto S’ → S. Poi vado a vedere S dove va: S → AB | aA. Possiamo continuare ad aggiungere le produzioni di A, ma poi ci fermiamo.

Formalmente:

Calcoliamo closure di I.

I = { S’ → S } J = I

• S’ → •S ⇒ S → •AB non appartiene a I ⇒ add
• ⇒ S → •aA non appartiene a I ⇒ add
• I = { S’ → •S, S → •AB, S → •aA }

Continuo:

• S → •AB → chi ci sta a destra del pallno? A. Quindi aggiungo tutta la roba di A a quello giá esistente: I = { S’ → •S, S → •AB, S → •aA, A → •bB, A → cAb, A → •a }

Continuo:

• S → •aA ⇒ non succede niente perché c’é a piccola, che é terminale.

Poi, aggiungiamo un pallino all’estrema sinistra di ogni parte destra di ogni produzione: { S’ → •S, S → •AB, S → •aA, A → •bB, A → cAb, A → •a }

Questo é il mio I0, ovvero il mio insieme di partenza. Da qua, mi calcolo tutti gli altri insiemi, facendomi la goto e la chiusura di ogni produzione.

Prendo tutti i simboli a destra del pallino, e me li metto in colonna quando vado a calcolare goto.

Il ragionamento qua é: chi é che produce •<simbolo> (nella parte a destra)?
Es. Nel primo caso: chi é che ha S nella parte destra dopo il pallino? Solo S’ → •S. Siccome sto facendo la goto, sposto il pallino a destra e poi mi calcolo la closure.

Nella chiusura devo SEMPRE includere l’insieme originale E le produzioni dopo il pallino.
Ad esempio clos( S → A•B), mi ritrovo dopo il pallino B, quindi aggiungeró B → •Bb ecc ecc

1. goto(I0, S) = clos({S’ → S•}) = { S’ → S•} ⇒ non abbiamo mai visto questo insieme quindi I1
2. goto(I0, A) = clos({S → A•B}) = { S’ → A•B, B → •Bb, B → •BA, B → •b }
3. goto(I0, a) = clos({S → a•A, A → a•})
4. goto(I0, b) = clos(A → b•B)
5. goto(I0, c) = clos(A → c•Ab)

NB: al passo 1, troviamo un qualcosa che ha giá il pallino alla sua estrema destra. Nonostante si tratti di un insieme che non abbiamo mai analizzato, non dobbiamo analizzarlo proprio perché il pallino é giá tutto a destra.

Poi basta, proprio come l’esercizio sulle chiusure, continuo sino a quando non trovo piu nulla di nuovo.

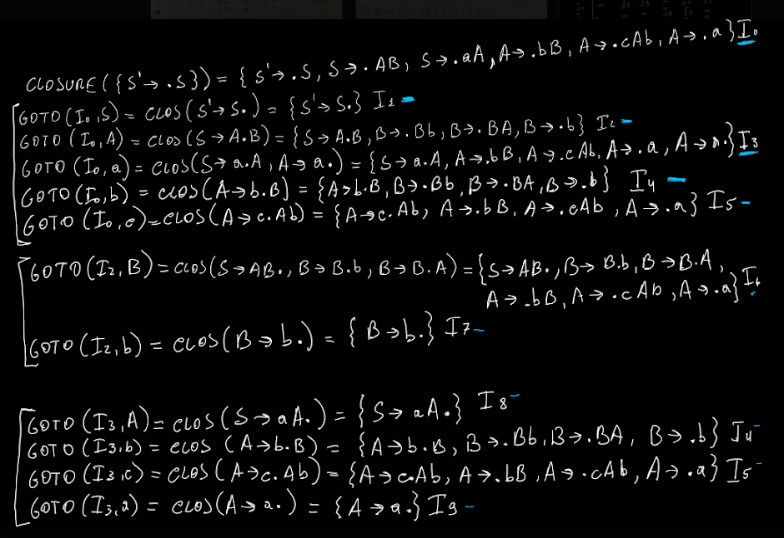
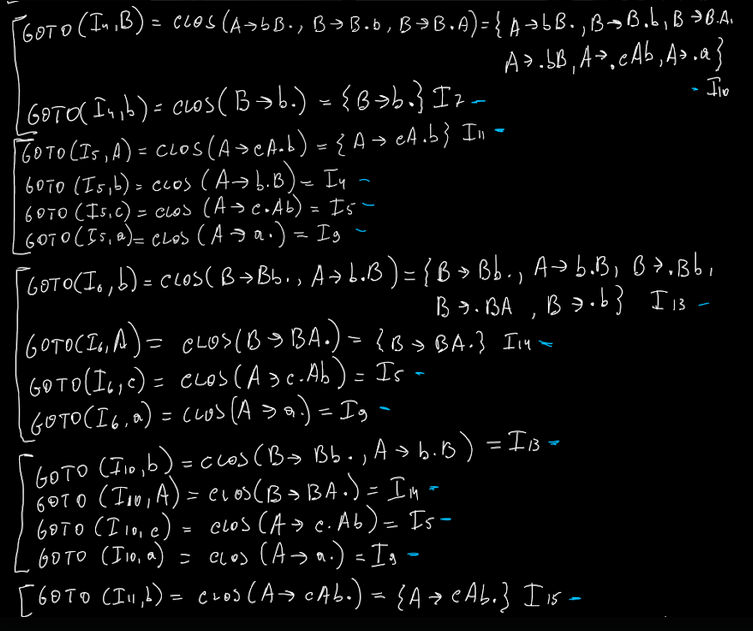
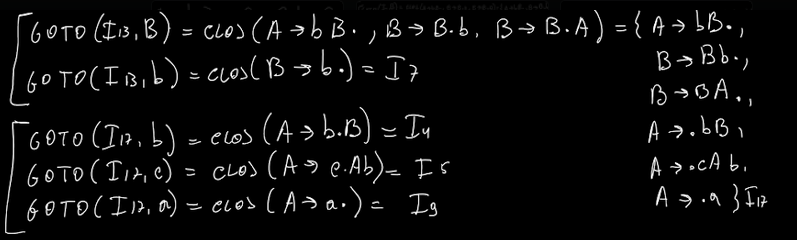
UN: Unify

Traccia

α1 × (α2 → α1) × (α1 → α2)
α3 × ((α2 → α1) → α3) × α4

Cosa bisogna fare

Anche qui seguiamo la “logica dei pronomi”.

Tre passi fondamentali:

1. albero astratto: molto semplice, stile “ADT” (vedi ER: passo 1)
2. stabilire ordine di visita DFS: la classica visità in profondità, basta solo ricordarsi che i “pronomi”
3. applicare la unify e scegliere i rappresentanti

Regolette

1. Albero astratto

   1. Per disegnare l’albero astratto parto sempre da x.
   2. L’associatività sta a sinistra, quindi conviene partire da destra verso sinistra
   3. NORMALMENTE salvo dove specificatamente indicato l’ordine di priorità è il seguente:
      • PRIMA le x
      • Poi i →
   4. NORMALMENTE salvo dove diversamente specificato, l’associatività è tutta a SINISTRA DI TUTTO
      • vale a dire: se ho ‘a1 x a2 x a3’ devo immaginarmele come ‘(a1 x a2) x a3’ come se a2 fosse in mezzo e decidesse a chi unirsi… quindi posso mettere le parentesi
   5. Quando sto disegnando l’albero, e noto che α1 l’ho già disegnato da qualche parte, devo fare un cerchio che va dall’originale alla posizione attuale (dovrei avrei disegnato α1).

2. Ordine DFS

   1. Quando stabilisco l’ordine di visita, non devo contare i “buchi” lasciati dai cerchi “al posto di α1”
   2. NON ESISTE UNA DFS UNICA

3. Unify e scelta del rappresentante - **** presi a coppie, si verificano questi casi:

   1. non si verifica mai
   2. 1 e 7 rappresentano lo stesso tipo (esempio, sono due α)
      1. scelgo uno dei due
   3. 1 e 7 sono operatori con due figli
      1. scelgo uno dei due
   4. 1 e 7, uno dei due è una variabile (è un α insomma)
      1. scelgo l’operatore

4. Scrivo le classi di equivalenza

   ---

Passo 1: disegno del type graph

Qui non c’è molto da spiegare, c’è bisogno di molta pratica.

Esercizio base “normale”

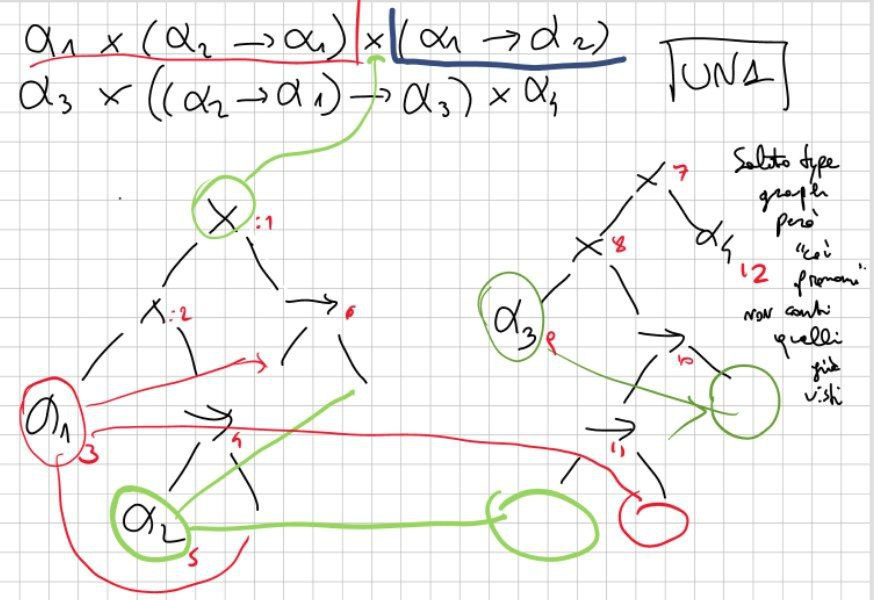
Esercizio difficile: priorità invertita (prima→ , poi x… normalmente è il contrario) e associatività a destra

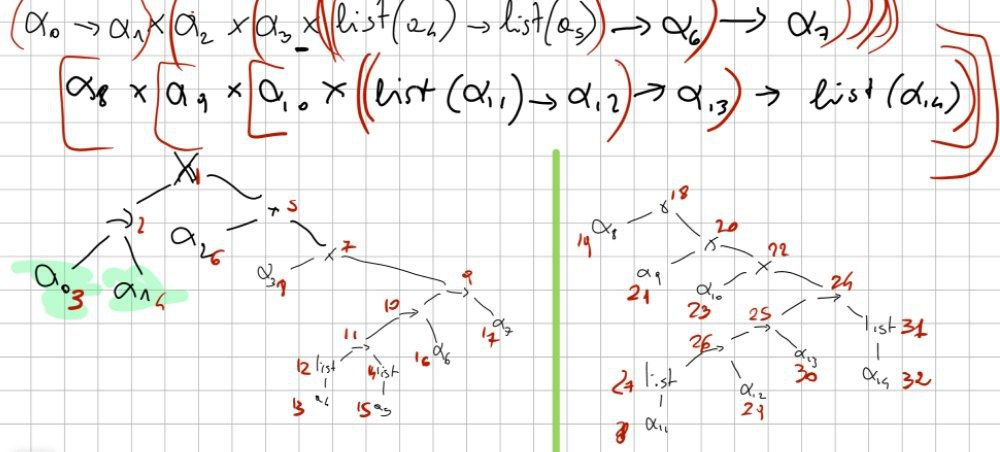
Passo 2: stabilire l’ordine di visita DFS

Lanciare una DFS e segnare l’ordine di vista accanto a ogni nodo. Ad esempio, x sarà il nodo radice, quindi scriverò 1 ecc

L’unica cosa da tener presente è che: quando ho un α già referenziata non la conto nella visita.

Questo passo è già segnato nell’immagine qui sopra.

Passo 3: chiamare la unify e scelta dei rappresentanti

Idealmente i due alberi vanno di pari passo. Devo analizzare i due alberi a coppie a partire dalle radici, e vedere cosa posso unire. Nel caso semplice si inizia dall’alto 1 e 7: sono le radici degli alberi.

Ecco i quattro casi seguiti dal criterio di scelta del rappresentante:

1. non si verifica mai
2. 1 e 7 rappresentano lo stesso tipo (esempio, sono due α)
   1. scelgo uno dei due
3. 1 e 7 sono operatori con due figli
   1. scelgo uno dei due
4. 1 e 7, uno dei due è una variabile (è un α insomma)
   1. scelgo l’operatore

Nel caso difficile devo prendo 1 e 18.

Risoluzione caso difficile:

****

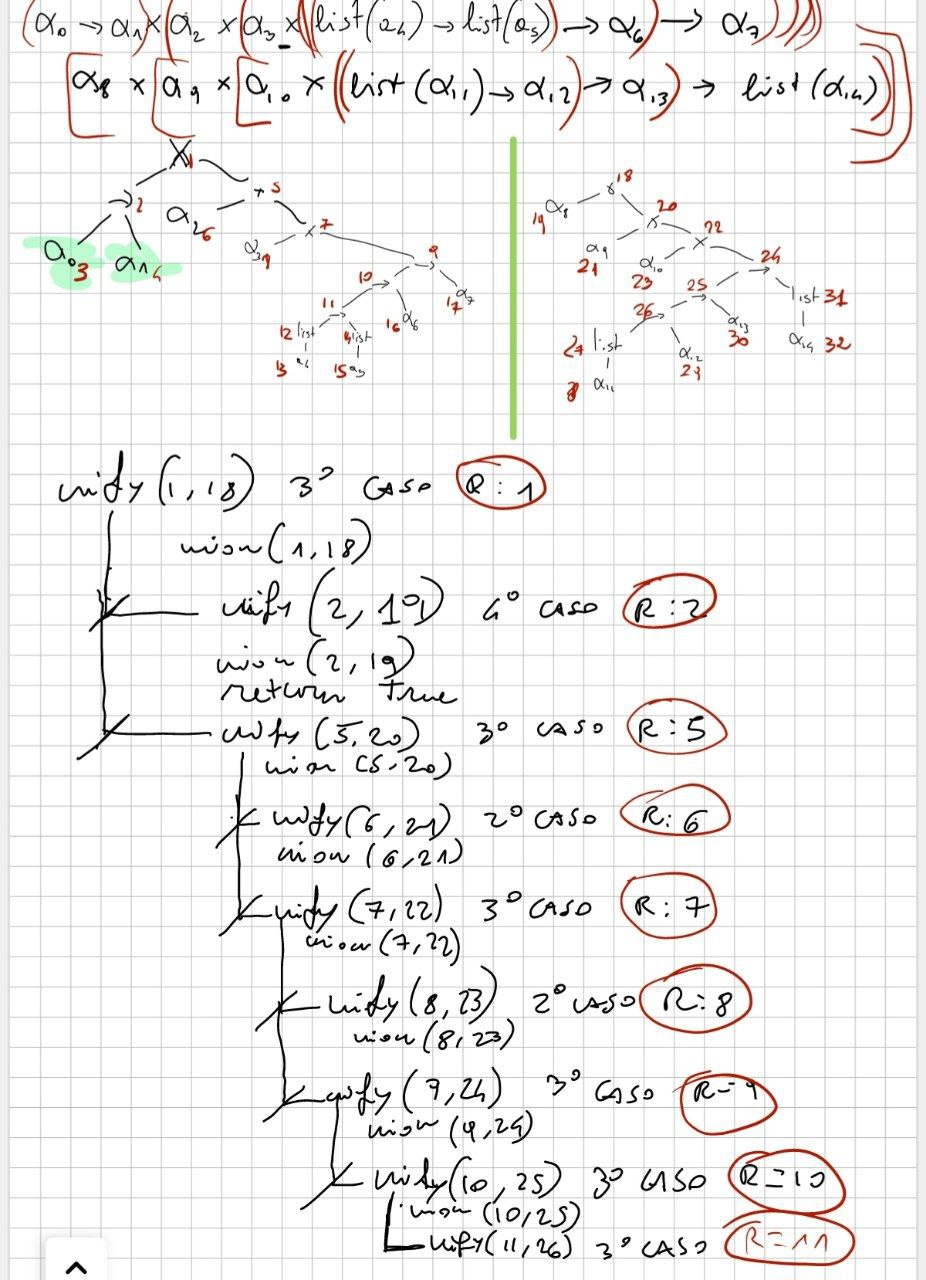
DEVO USARE l’approccio grafico, quindi non occorre riscrivere tutto da capo.

Qui sopra, una possibile soluzione con approccio grafico del caso difficile.

Passo 4: scrivere le classi di equivalenza

Per l’esercizio semplice, le classi di equivalenza ottenute sono:

{{1,7}, {2,8}, {3,9}, {4, 10}, {5,11}, {6,12}}

Scrivere in alto, sopra ogni classe, i vari rappresentanti presi prima, per ogni classe di equivalenza (1 2 3 4 11 e 6).

---

Per l’esercizio difficile basta fare la stessa cosa.

DOM

Traccia

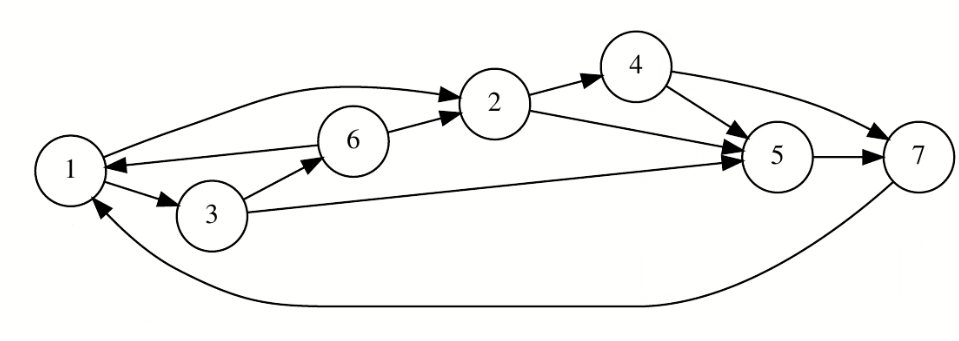
Regolette

1. DFS, Post-Order, e Reverse PostOrder
   1. DFS come ti pare. Fai la classica se non sai come farla.
2. Post-order
   1. Come ti pare, fai la visita per livelli a partire dall’ultimo se non sai come fare.
3. Reverse post-order (RPO)
   1. Riscrivi questo ordine al contrario
4. DOM(nodo partenza) = 1, DOM(2) = … = DOM(9) = {2, …, 9}
   1. Cominci ad applicare algoritmo DOM: per ogni nodo seguendo la RPO, vedi chi sono i predecessori e:
      1. se è uno, fai DOM(predecessore) U elemento attuale (es. ordine 2, 3, DOM(3) = PREDS(3) = {2} ⇒ devo mettere DOM(2) + 3 ⇒ {2, 3}
      2. se è più di uno, fai intersezione (roba comune) tra gli elementi comuni e poi unisci quello attuale

QA

• la DFS mi viene diversa, come faccio?
  • NON ESISTE UNA DFS UNICA
• il POST-ORDER mi viene diverso, come faccio?
  • NON ESISTE UN POST ORDER UNICO. Di solito si fa la visita per livelli partendo dall’ultimo.

Svolgimento

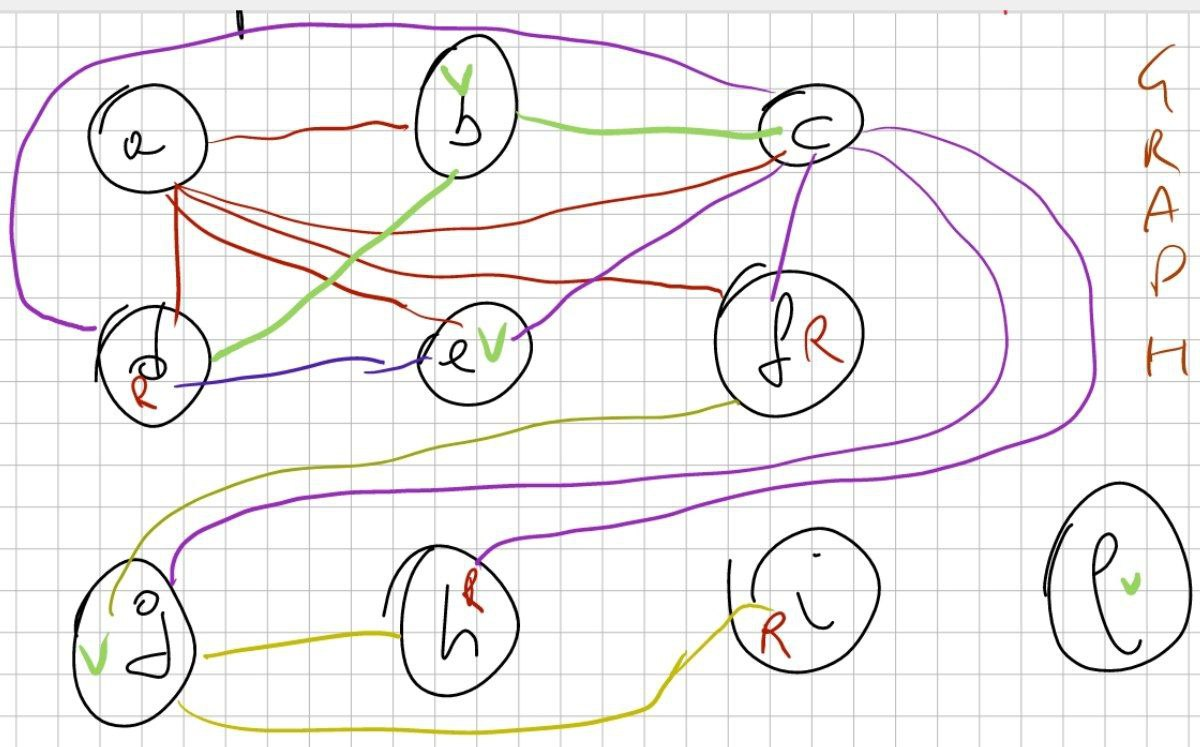
IG: Inference Graph - colorazione grafo

Traccia

Dato il seguente BB in 3AC I costruire l’interference graph I applicare all’IG l’algoritmo di colorazione specifico per la register selection con k = 2

• a=1
• b=2
• c=a+1
• d=a+4
• e=b+1
• f=e+d
• g=a+2
• h=f+g
• i=c+6
• l=g+2

Passi

1. Disegnare il grafo
2. Eliminare i nodi uno ad uno
3. Colorare il grafo

Regolette

Dalla traccia k = 2, abbiamo i seguenti casi:

1. un nodo ha il minor numero di archi (o nessuno) < k → ottimo, lo elimino
2. altrimenti, se ho più nodi che hanno tutti numero di archi >= k → elimino il nodo con il maggior numero di archi in assoluto in tutto il grafo
   In altre parole: quando non posso fare nulla (la condizione è MINORE di k, non MINORE UGUALE) tolgo il nodo con più archi in assoluto.

Passo 1: disegno tutto il grafo

Disegnamo tutti gli stati a b c d e f g h i l

Innanzitutto vediamo a: dobbiamo trovare l’ultima occorrenza di a: appare in g. Quindi devo collegare a con tutti gli “stati” che vengono DOPO sè stesso e prima di g (g escluso). Ripeto per tutti gli stati.

ESEMPIO: c lo collegherò con gli “stati” d, e, f, g, h perchè inizio da d e compare l’ultima volta in i.

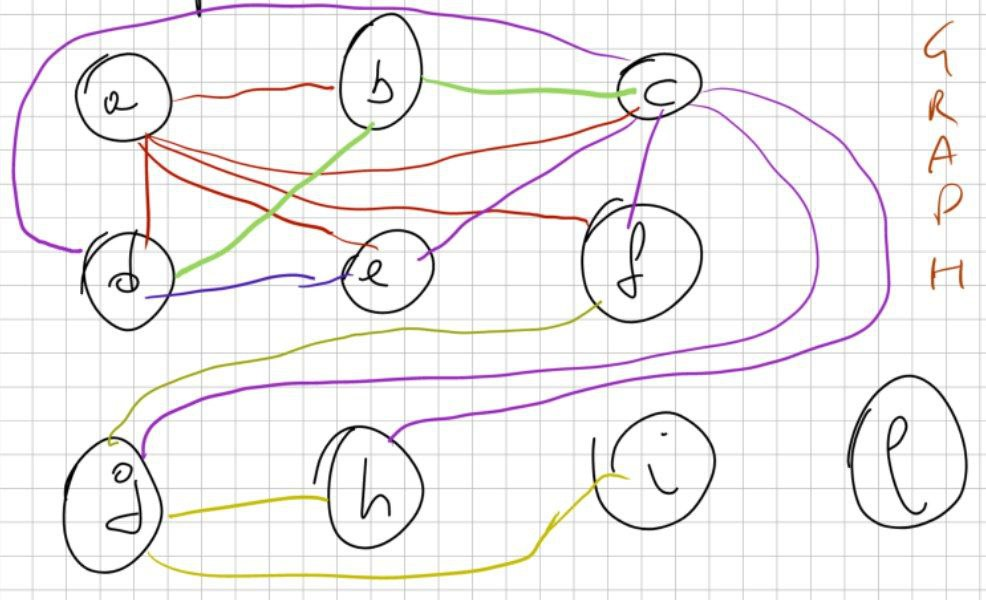
Passo 2: eliminare i nodi uno ad uno

Adesso: l’obiettivo è quello di eliminare pian piano tutti i nodi. Dalla traccia k = 2.

Iniziamo: chi è che ha il minor numero di archi in assoluto? il nodo l (è una L).

Ridisegnamo il grafo, facendo una bella croce su l.

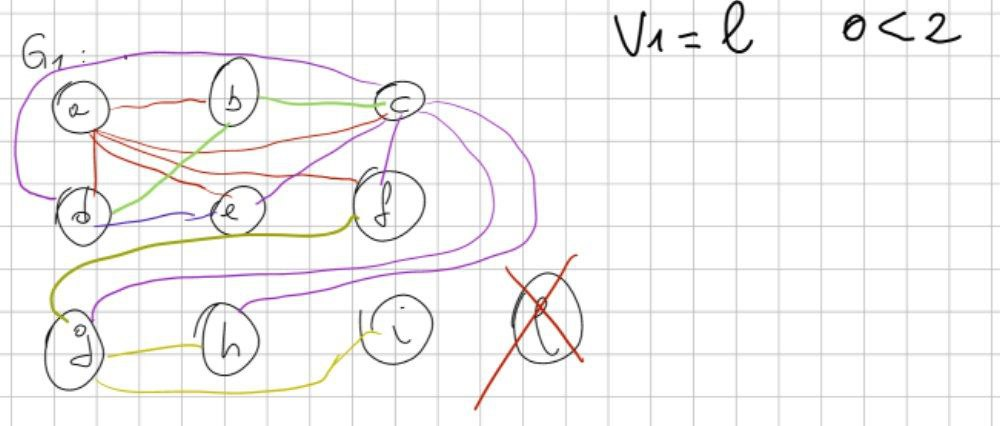
Rimuoviamo tutti gli archi di l e andiamo a ridisegnare il grafo.

Passo successivo: qual è il nodo con il minor numero di archi? i naturalmente, poiché ha solo un arco.

Rimuoviamo allora i. (caso

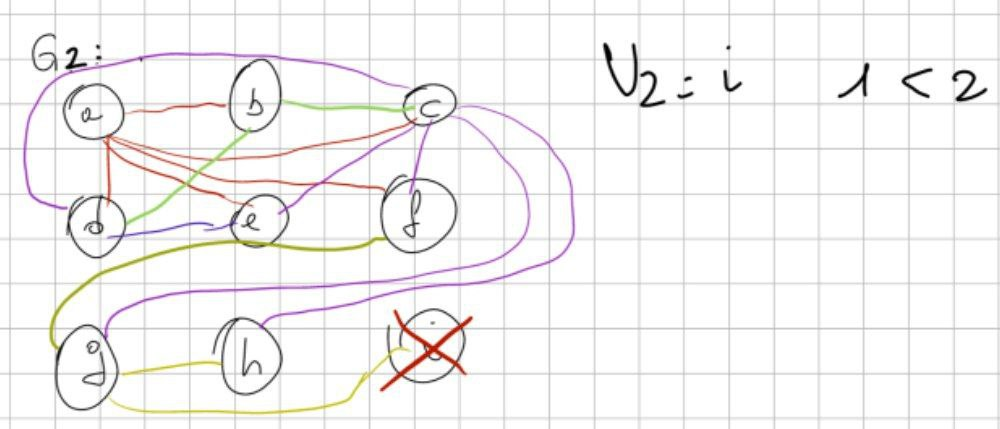
Passo successivo: qual è il nodo col minor numero di archi? Eh, ma qui c’è il caso 2: infatti la condizione è MINORE DI 2, NON minore uguale a 2. Quindi stiamo nel caso 2.

Il caso 2 ci dice “prendi quello col maggior numero di archi e toglilo.

In questo caso è C, perché ne ha 7, e quindi tolgo C. Ci scrivo però anche un bel “TOSPILL” a destra. È importante!

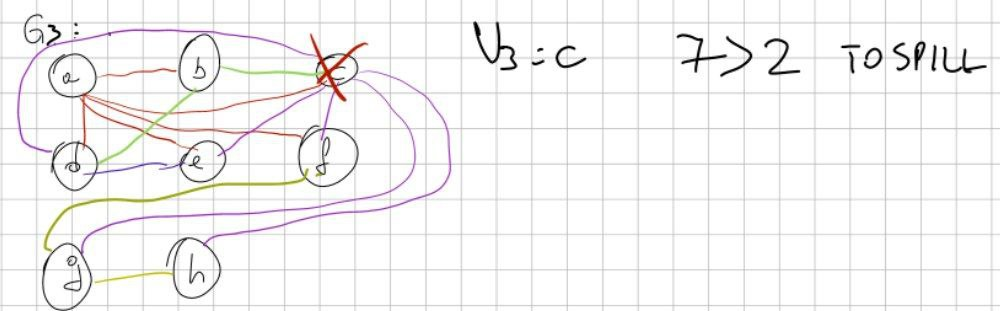
Proseguo finché non arrivo alla fine.

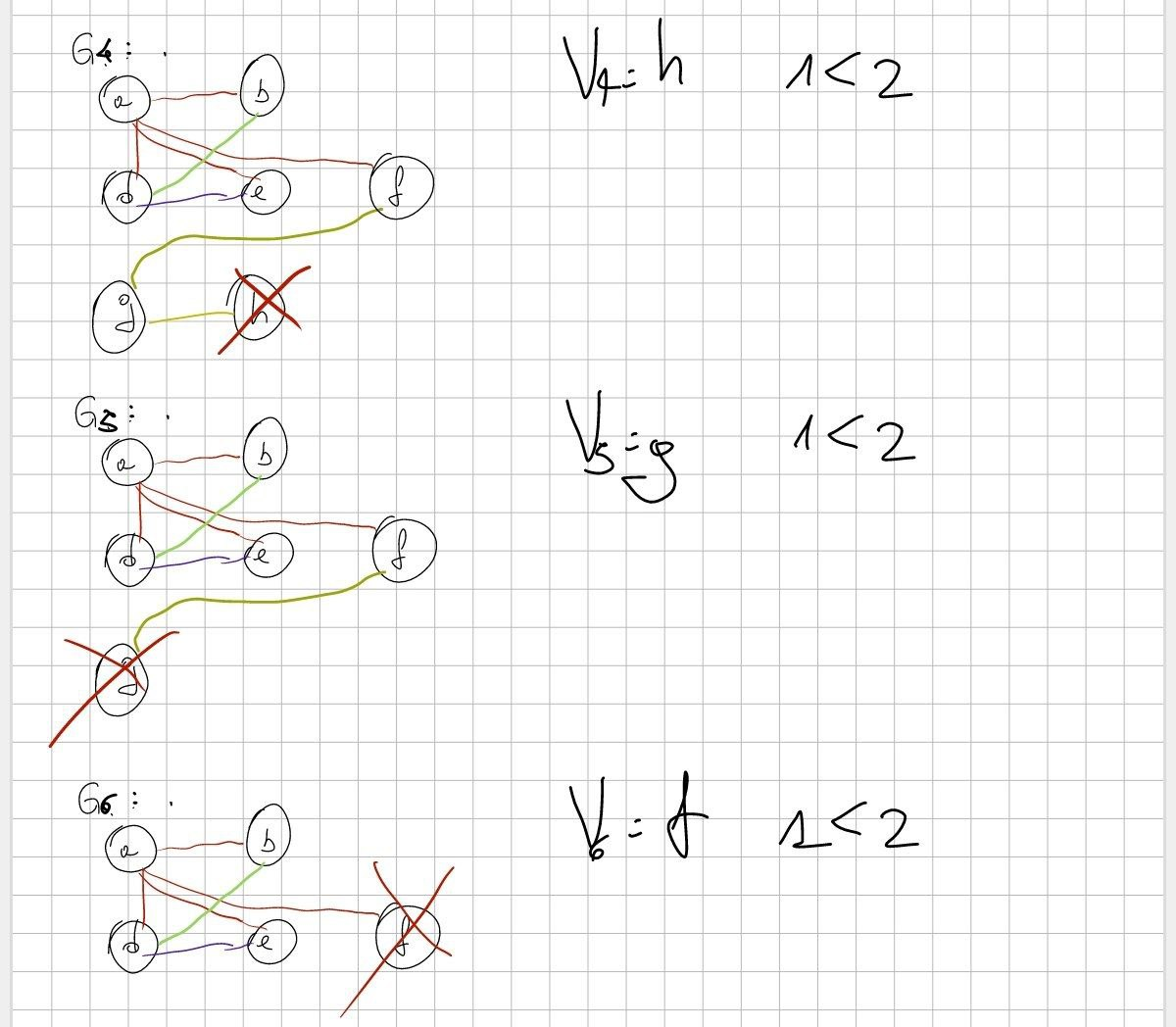
Qua c’è un altro TOSPILL da fare!

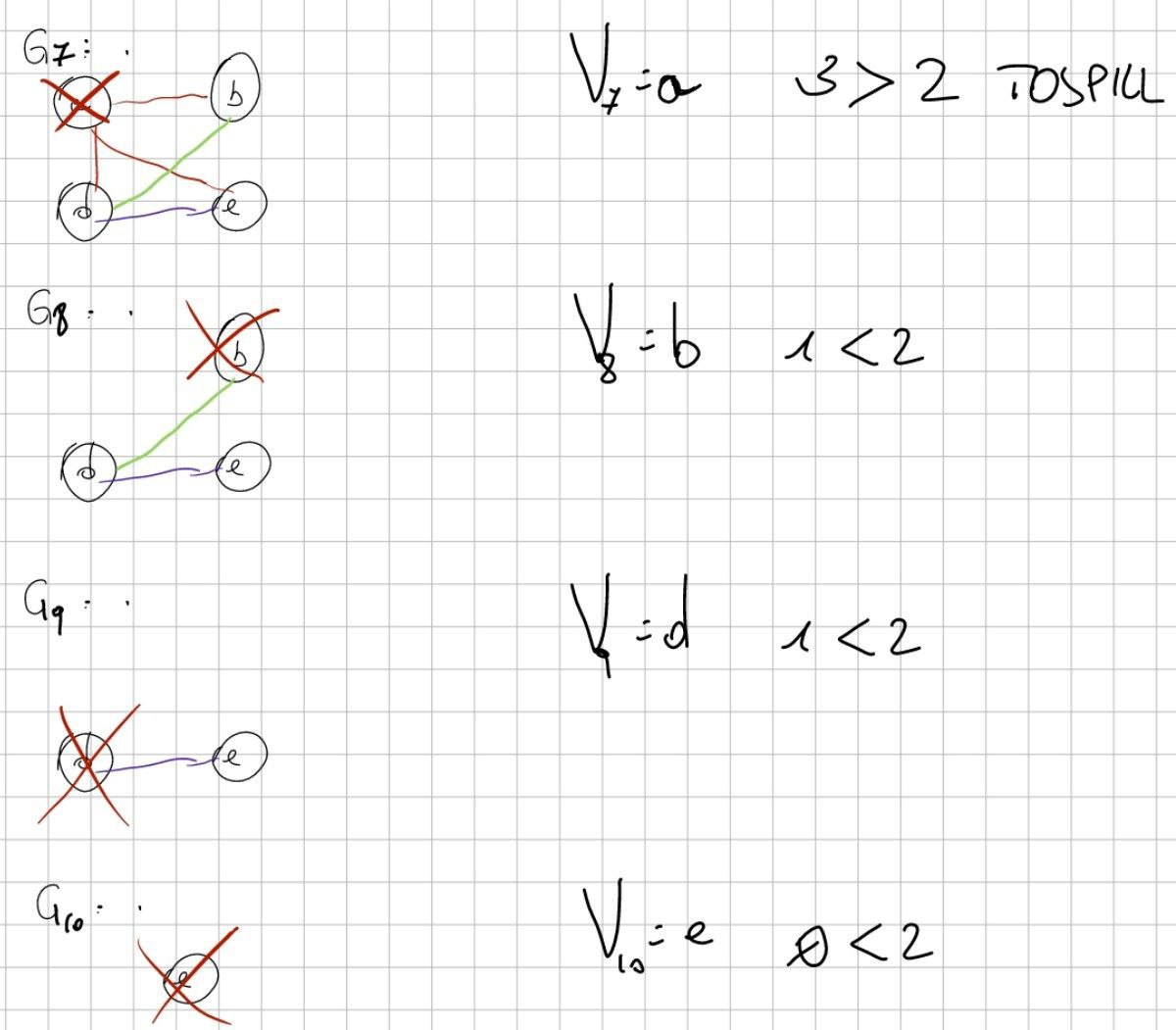
Finalmente ho finito!

Passo 3: coloro il grafo

Parti dalla fine (G10).

Regolette:

1. all’inizio, il primo nodo avrà il colore che preferiamo (es. rosso)
2. il nodo successivo, dovrà avere un colore diverso da quello vicino
3. i TOSPILL sono incolori!

Quindi:

• a V10 (e) assegno verde
• a V9 (d) assegno rosso dato che l’adiacente è verde
• a V8 (b) assegno verde, poiché il rosso l’avevo già assegnato
• a V7 (a) non assegno alcun colore: c’è il tospill
• a V6 (f) assegno rosso
• a V5 (g) assegno verde, poiché il rosso l’avevo già assegnato
• a V4 (h) assegno rosso, poiché il verde l’avevo già assegnato
• a V3 (c) non assegno alcun colore: c’è il tospill
• a V2 (i) assegno rosso, poiché il verde l’avevo già assegnato
• a V1 (l) assegno verde (ma posso anche assegnare il rosso)

NOTA BENE: per la buona riuscita di questo esercizio, è opportuno segnarsi sul grafo di partenza i colori → questo perché può essere utile vedere a colpo d’occhio chi è adiacente a chi.

Non richiesto dall’esercizio, ma riportato comunque per comodità, ecco la colorazione del grafo finale:

ER: Erschev e assembly

Regolette

• prendi il testo dell’esercizio
• costruisci un albero facendo dfs, utilizzando ultima riga. Ignori i valori istantanei.
• fai una dfs e devi seguire l’algoritmo:

• generi il codice, prendi tutto, lo metti in lista et voilà!

Esercizio e albero

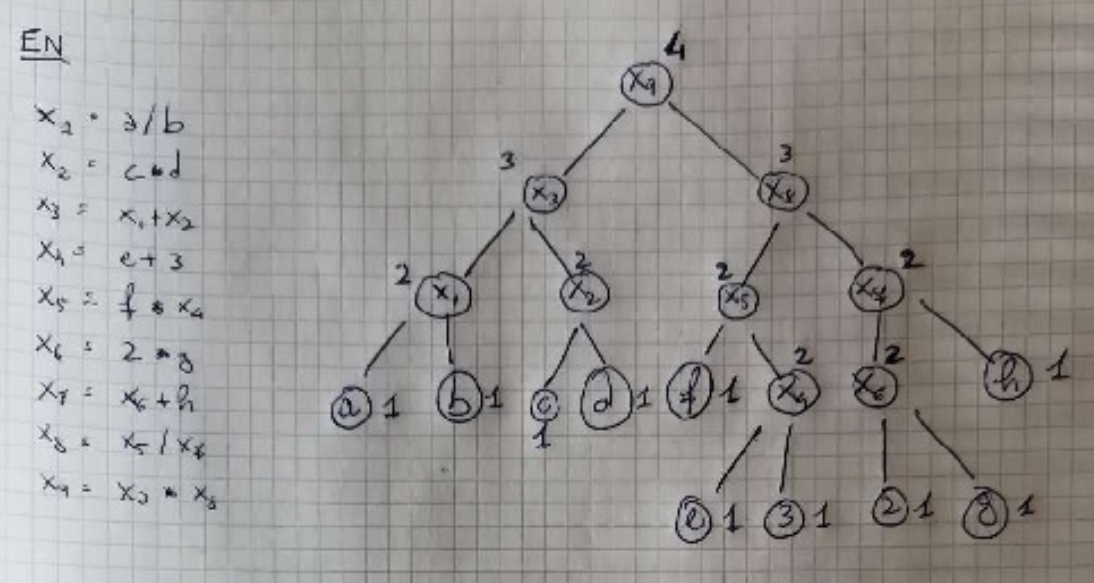
Risoluzione

Tracce di esercizi vari

Tracce di esercizi vari

ER

1. Costruire NFA per questa espressione (010)*(11)*
   1. 0 e 1 separati
   2. 01
   3. 0 separato
   4. 010
   5. 010*
   6. 1 e 1 separati
   7. 11
   8. (11)*
   9. fare merge di tutto
2. Costruire NFA per questa espressione ((a|c)*(cb))*
3. Costruire NFA per questa espressione ((11|00|11)*(0|1)*)*
4. Costruire NFA per questa espressione (x|yx)*(zy|x)*
5. Costruire NFA per questa espressione ((a|b)c)*|(cb|a)*

NFA

Usare subset construction per costruire DFA a partire da NFA

+-------+---------------------------+
| Stato |        Transizioni        |
+-------+---------------------------+
|   0   | a → 0                     |
|       | b → 0                     |
|       | ε → 1, 2                  |
+-------+---------------------------+
|   1   | a → 1                     |
|       | ε → 3                     |
+-------+---------------------------+
|   2   | b → 2                     |
|       | ε → 3                     |
+-------+---------------------------+
|   3   | c → 3        (terminante) |
+-------+---------------------------+

+-------+------------------------------+
| Stato |          Transizioni         |
+-------+------------------------------+
|   0   | c → 0, 1                     |
+-------+------------------------------+
|   1   | (terminante)                 |
+-------+------------------------------+
|   2   | b → 2                        |
|       | c → 3                        |
+-------+------------------------------+
|   3   | a → 3, 1                     |
|       | ε → 0                        |
+-------+------------------------------+

+-------+---------------------------------------------+
| Stato |                 Transizioni                  |
+-------+---------------------------------------------+
|   0   | a → 0, 2                                     |
|       | b → 0                                        |
|       | ε → 1                                        |
+-------+---------------------------------------------+
|   1   | c → 1, 2                                     |
+-------+---------------------------------------------+
|   2   | b → 2, 0                                     |
|       | ε → 3                                        |
+-------+---------------------------------------------+
|   3   | a → 3                                        |
|       | c → 4                                        |
+-------+---------------------------------------------+
|   4   | b → 4                                        |
|       | ε → 1                                        |
|       | (terminante)                                 |
+-------+---------------------------------------------+

+-------+----------------------------------+
| Stato |            Transizioni           |
+-------+----------------------------------+
|   0   | y → 0                            |
|       | x → 1                            |
|       | ε → 3                            |
+-------+----------------------------------+
|   1   | z → 2                            |
|       | x → 0                            |
+-------+----------------------------------+
|   2   | x → 1                            |
|       | ε → 3 (terminante)               |
+-------+----------------------------------+
|   3   | z → 2                            |
|       | ε → 0                            |
+-------+----------------------------------+

MIN

+-------+-------------------------------+
| Stato |          Transizioni          |
+-------+-------------------------------+
|   0   | a → 3                         |
|       | b → 2                         |
+-------+-------------------------------+
|   2   | b → 2                         |
|       | a → 3                         |
+-------+-------------------------------+
|   3   | b → 4                         |
|       | a → 1                         |
+-------+-------------------------------+
|   1   | a → 1                         |
|       | b → 4                         |
+-------+-------------------------------+
|   4   | a → 4                         |
|       | b → 4                         |
|       | (terminante)                  |
+-------+-------------------------------+

RIC

A --> Ba|a
B --> Cb|b
C --> Cc|A

A --> BC|Ab|a
B --> Ad|CA|BA
C --> Bc|AC|CA|c

A --> BaA|Ac|a
B --> Ae|CbB|BB|b
C --> BCa|DdA|CCe
D --> DC|epsilon

X --> XaZ|YWc|W
Y --> Yd|WbZ|ZWc|X
W --> WXa|ZZd|YYe|c
Z --> XX|Zc

A --> BC|Ab|a
B --> Ad|CA|BA
C --> Bc|AC|CA|epsilon

FAT

A --> AaCb
   AaCa
   ABc
   BVbB
   BAC
   BVbC
   aa
   a

B --> CbC
   CAa
   CbA
   BAc
   BAb
   epsilon

C --> CBa
   AaC
   CBC
   BaB
   BaA
   c

A -> AaBC
   AaB
   AaCC
   AaB
   a

B --> BbC
   BBB
   BbB
   b

C --> Cc
   CCc
   CcC
   c

BU1 LR(0)

S' --> S
S --> AB
   aA

A --> bB
   cAb
   a

B --> Bb
   BA
   b

UN

1. $${\alpha }_1\times ({\alpha }_2\to {\alpha }_1)\times ({\alpha }_1\to {\alpha }_2)$$

\

\alpha_3 \times ((\alpha_2 \rightarrow \alpha_1) \rightarrow \alpha_3) \times \alpha_4

$$2.$$

\alpha_1 \rightarrow \left( \alpha_2 \rightarrow \left( \alpha_2 \times (\alpha_3 \rightarrow \alpha_1) \right) \right)

(\alpha_4 \times \alpha_5) \rightarrow \left( \alpha_4 \rightarrow (\alpha_5 \times \alpha_3) \right)

$$3.$$

\alpha_1 \times \left( (\alpha_2 \rightarrow \alpha_3) \rightarrow \text{list}(\alpha_4) \right)

\left( (\text{list}(\alpha_5) \times \text{list}(\alpha_6)) \rightarrow \alpha_7 \right) \rightarrow \text{list}(\alpha_8)

### DOM 1. ``` +-------+-------------------------+ | Stato | Transizioni | +-------+-------------------------+ | 1 | → 3, 2 | +-------+-------------------------+ | 2 | → 5 | | | → 4, 6 | +-------+-------------------------+ | 5 | → 1 | +-------+-------------------------+ | 6 | → 2 | +-------+-------------------------+ ``` ### IG 1. ``` a = 1 b = 2 c = 3 d = a + c e = b + a f = c + d g = b + 3 h = a + 1 ```