02 - Performance evaluation and classification

Overview

• Description:: Performance evaluation of ML is important, K-Fold Cross Validation is a general prototype method to evaluate classification problems, several metrics can be used, estimation is very useful also during the execution of an algorithm

RIGUARDARE I PRIMI 25 MINUTI dove fa il riassunto!!!

1. We have a H hypotetical space
   • it’s too generic! So we restrict to H’
2. Now we have H’ → H : it is called language restriction
   • here we can take h*, that is the “best possible hypotesis” (known as search bias) WE MAKE A RESTRICTION!

The matter

h*(x’) = f(x’)

but we don’t know f(x’)!

Measure the performance of my solution

Errors

True error

Probability that extracting one sample from the input I have a mistake between the hypotesis the solution I am measuring and the true value of the function.

$erro{r}_D(h)\equiv P{r}_{x\in D}[f(x)\ne h(x)]$

This our target error that it is impossible to compute since we don’t know f(x).

Sample error

Defined on a dataset S, a set of samples for which we have both input and output, so for given S we can actually define sample error as an error that is the number of errors divided by the size of S.

$erro{r}_S(h)\equiv \frac{1}{n}{\sum }_{x\in S}\delta (f(x)\ne h(x))$ We can compute this one! but only on a small data sample.

It is important that sample error is a good approximation of the true error.

We can guarantee this by finding a bias, that is computed as the difference between E(errorS(h)) and errorD(h). We are looking for the 0 value. To be highly guaranteed, the bias should be 0!

• E[errorS(h)]: This represents the expected (average) error of the model h across all possible training datasets S. In other words, it’s the average error that h would make when trained on different subsets of the data S.

• errorD​(h): This represents the error of the model h on a specific test dataset D. It’s the error that h makes when applied to the specific dataset D.

Too much data doesn’t approximate in a good way, so we can get a trade off: 2/3 for training, 1/3 for testing.

Overfitting

hypotesis h to H overfits training data if there is an alternative hypothesis h’ t H such that errorS(h) < errorS (h’) and errorD(h) > errorD(h’)

K-Fold Cross Validation

• repeats validation several times

1. take all dataset and split into several parts
2. for each part, I use that part as test set and the remaining as training
3. the output of the error is the average of the errors

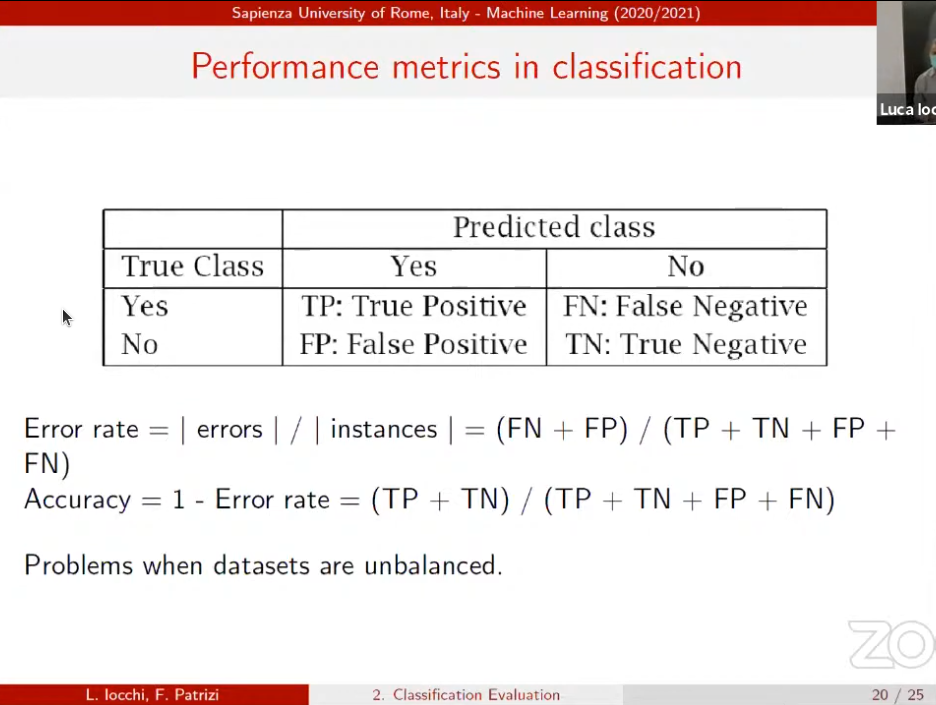
Not always we want to use unbalanced datasets! ex. classification problem +,-

this slide is also super important! exam question!

This one is for balanced datasets

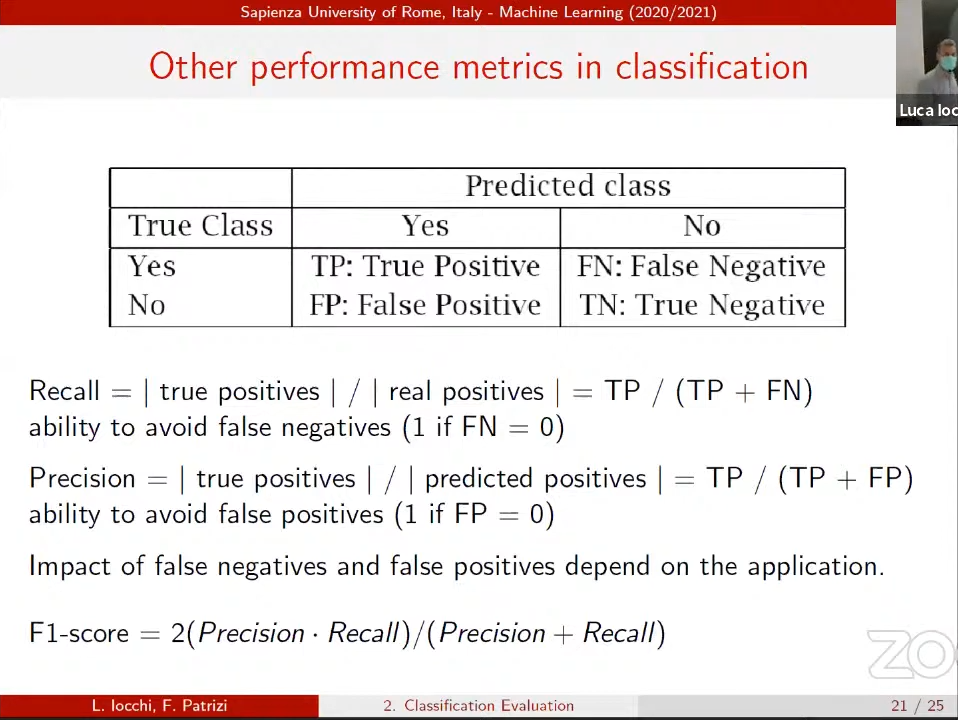
There also be a Confusion Matrix: for each subset, I mark when a subset is recognized as another one.