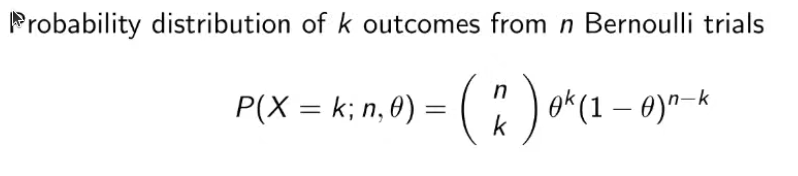05 - Bayesan Learning

Overview

• Description:: define a ML in terms of distribution, probabilistic approach

Probabilistic estimation

Given D and H: P(H|D): we know the dataset and want to estimate the probability of an hypothesis

This is called posterior probability: it is the probability of h after we see the data.

$$P(h|D)=\frac{P(D|h)\cdot P(h)}{P(D)}$$

P(h) = prior probability of hypotesis h P(D) = prior probability of training data D P(h|D) = prob of h given D P(D|h) = prob of D given h

MAP Hypothesis

Given any function, the argmax is the highest point a function reaches on the x axe.

Maximum a posteriori hypotesis $h_{MAP}$

$h_{MAP}\equiv argma{x}_{h\in H}P(h|D)=argma{x}_{h\in H}\frac{P(D|h)P(h)}{P(D)}=argma{x}_{h\in H}P(D|h)P(h)$

We don’t need to divide for P(D) because it is a constant!

• assuming that if the hypothesis are a priori uniformly distributed

Maximum Likelihood (ML) $h_{ML}=argma{x}_{h\in H}P(D|h)$

Important

When we have information about priors, we use MAP Hypothesis, if we can assume that all hypothesis have uniform priori distribution we can use ML Hypothesis

• example
  • h1, h2, h3
    • P(h1|D) = 0.4
    • P(h2|D) = 0.3
    • P(h3|D) = 0.3
  • given a new istance
    • h1(x) = +
    • h2(x) = -
    • h3(x) = -

If we consider HMAP it will predict + But if we use the contribution of all hypothesis then the negative prediction is better in terms of result.

So it is not convenient HMAP

Bayes Optimal Classifier

Consider target fn f: X → V, V={v1, …, vk}, Dataset D, $x\notin D$ $P(Vj|x,D)={\sum }_{x_i\in H}P(v_j|x,h_i)P(h_i|D)$

total probability over H

The best prediction for x will be the argmax of this

Optimal means that it optimally solves the problem we stated at the beginning.

It is a theoretical model, that unfortunately cannot really be applied unless we have a very small cases.

Example

1. 10% are h1: 100% cherry
2. 20% are h2: 75% cherry, 25% lime
3. 40% are h3: 50% cherry, 50% lime
4. 20% are h4: 25% cherry, 75% lime
5. 10% are h5: 100% lime

We choose a random bag (we dont know the type) and extract some candies from it. What kind of bag is it? What is the probability of extracting a candy of a specific flavor next?

Ok, now we must find prior probab distribution: 0.1, 0.2, 0.4, 0.2, 0.1

Likelihood for lime candy (probability of dataset given hypothesis): P(I|H) = 0, 0.25, 0.5, 0.75, 1

Applying the formula to extract a lime candy: ${\sum }_{h_i}P(I|h_i)P(h_i)=0\ast 0.1+0.25\ast 0.2+0.5\ast 0.4+0.75\ast 0.2+1\ast 0.1=0.5$ Now we don’t have any dataset, so dataset is empty.

Let’s assume we get a lime candy.

We want to compute the probability distribution of the hypothesis given this dataset:

The usual thing, but $\alpha$ is known as “normalization factor”.

How to calculate alpha? $\alpha =P(D1)={\sum }_{i}P(D1|h_i)\times P(h_i)$ $=0\times 0.1+0.25\times 0.2+0.5\times 0.4+0.75\times 0.2+1\times 0.1$ $=0+0.05+0.2+0.15+0.1$ $=0.5$

Same goes for the second candy: The blue arrow: we computed that in the previous step The red segment: is only the usual thing to multiply

Same goes for the third candy? If we consider the approach of $H_{MAP}$ and it is H5 in this case, it would be 1. It is not correct!

So, we compute the sum of the probabilities to extract lime among all the possible hypothesis. 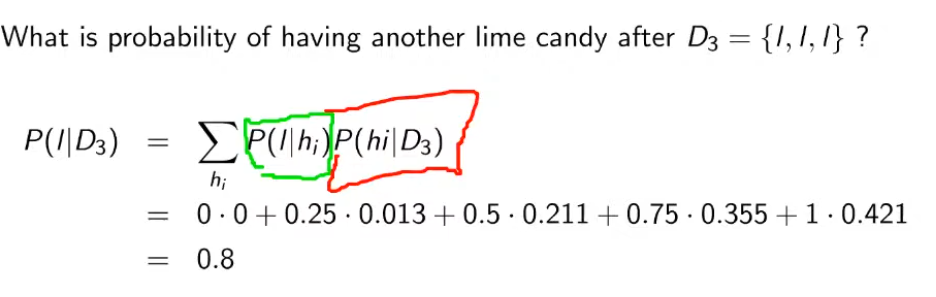(we don’t count the first, because is 0!)

Bernoulli distribution

$P(X=k)=p^k\times (1-p{)}^{1-k}$

The Bernoulli distribution is a discrete probability distribution representing two possible outcomes - often referred to as success and failure.

Imagine you are tossing a fair coin. The outcome can be either heads (success) or tails (failure). This situation perfectly fits the Bernoulli distribution because there are only two possible outcomes, and each outcome has a fixed probability.

For example, if the coin is biased and the probability of getting a head (p) is 0.7 (and hence the probability of getting a tail is 1−p=0.31−p=0.3), the PMF for this unfair coin would be:

p & \text{if } k = 1 \text{ (success)} \\ 1 - p & \text{if } k = 0 \text{ (failure)} \end{cases}$$ In this case, the probability of getting heads (P(X=1)P(X=1)) is 0.7, and the probability of getting tails (P(X=0)P(X=0)) is 0.3. #### General approach ![[Screenshot_20231005_174347.png]] #### More Bernoulli (ex. coins) ![[Screenshot_20231005_174319.png]]