04 - Probability in ML

Overview

• Description:: revising general probability concepts

Revising

• we want to learn a function f: X → Y
• we have a dataset D = {(…)}
• we have a hypotesis space H where we want to search the best possible value

Probability

• we model probability of an action to determine what’s the best choice
• this is done because we hate to take decisions that are not suitable for our cases
  • ex. how much time should we leave before departing from a place in the airport

Elements of probability

Probability space

• $\Omega :samplespace$
• $\omega \in \Omega$ is a sample point / possible word / outcome of a random process…

A probability space (or probability model) is a function $P:\Omega \to R$ such that

• 0 ⇐ P(w) ⇐ 1
• ${\sum }_{w\in \Omega }$ P($\omega$) = 1

Example: rolling a die $\Omega =1,2,3,4,5,6$ $P(\omega )=\{1/6,1/6,1/6,1/6,1/6,1/6\}$ An event is any subset of $\Omega$ Probability of an event A is a function assigning to A a value in [0,1]

examples:

• A1 = “die roll < 4”: A1 = $\{1,2,3\}\subset \Omega$
  • P(A1) = P(1) + P(2) + P(3) = 1/6 + 1/6 + 1/6 = 1/2
  • (they are all indipendent events!. Obviously a single dice roll could result in just one of those probabilities, therefore is + not *)

Random variable

A random variable is a function that maps sample space $\Omega$ to some range (the reals, or Booleans…) $X:\Omega \to B$

Example: $Odd:\Omega \to B$

X is a variable and a function!

X = $x_i$ the random variable X has the value $x_i\in B$ X = $x_i$ is like saying $\{w\in B|X(\omega )=x_i\}$

Example: Odd = true → {1,3,5}

We can compute the probability of a random variable, by summing all the possible values belonging to the subset.

In the odd example is 1/2 because 1/6+1/6+1/6

Propositions

We can use logical operations to create propositions, using ^, V, not

We assume any event in a proposition is positive, therefore true, unless we use the NOT operator.

We have three operators:

• $\wedge$ is *
• V is +
• $┐$ is - (it means false)

Distributions

Probability distribution is a function assigning to a probability value to all possible assignments of a random variable.

Important

Sum of all values MUST BE 1

Join probability distribution: given two dices (fair), what’s the odd to get 3 on the first and 3 on the second? The first is 1/6, the second is 1/6, they are all separate events, so I just need to multiply each other probability, therefore the answer is 1/36

Also known as $P(X=x,Y=y)$ In ML I create a table rxc, row x columns, and write down all possible probabilities. The sum of each row and each column must be 1.

Conditional probability

A measure of the probability of an event happening, given that another event has already occurred

The formula is:

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

In the ML example $P(Cavity=true|Weather=sunny)$

The meaning of the formula is “what’s the probability of A KNOWING that B has happened?”

Total probabilities

$$E(X|Y)=\sum _{y_i\in D(Y)}P(X|Y=y_i)\times P(Y=y_i)$$

Chain rule

Example: Card Drawing Game

Suppose you have a standard deck of 52 playing cards. You draw three cards one by one without replacement. Let’s define the events:

• Event A: The first card drawn is a heart.
• Event B: The second card drawn is a face card (jack, queen, or king).
• Event C: The third card drawn is red.

Using the chain rule, the probability of these three events happening in sequence is calculated as follows:

$P(A\cap B\cap C)=P(A)\times P(B|A)\times P(C|A\cap B)$

1. Probability of Event A (Drawing a Heart): There are 13 hearts in a deck of 52 cards, so $P(A)=\frac{13}{52}=\frac{1}{4}$

2. Probability of Event B Given A (Drawing a Face Card Given the First is a Heart): After drawing a heart, there are 12 face cards left in a deck of 51 cards, so $P(B|A)=\frac{12}{51}=\frac{4}{17}$

3. Probability of Event C Given A and B (Drawing a Red Card Given the First Two Conditions are Met): After drawing a heart and a face card, there are 24 red cards left in a deck of 50 cards, so $P(C|A\cap B)=\frac{24}{50}=\frac{12}{25}$

Now, applying the chain rule:

$P(A\cap B\cap C)=\frac{1}{4}\times \frac{4}{17}\times \frac{12}{25}=\frac{48}{1700}=\frac{12}{425}$

So, the probability that the first card is a heart, the second card is a face card given that the first card is a heart, and the third card is red given the first two conditions is ($\frac{12}{425}$ ) or approximately ( 0.0282 ) (or ( 2.82% ).

Inference by enumeration

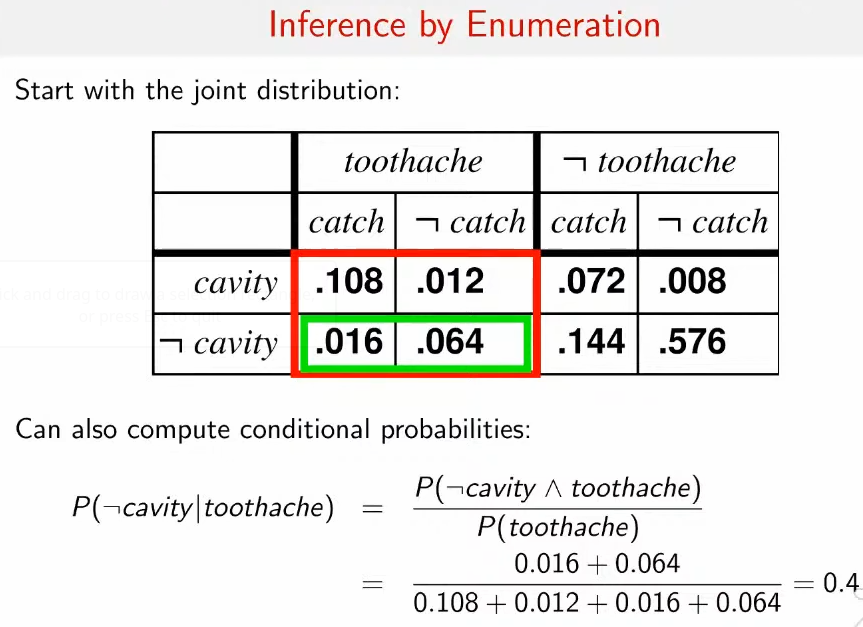
Conditional indipendence

• like the distributive law $P(X|Y,Z)=P(X|Y,Z)P(Y|Z)=P(X|Z)P(Y|Z)$

Product rule and Bayes

$P(a\cap b)=P(a|b)P(b)=P(b|a)P(a)$

⇒ from here we derive Bayes Rule

$P(a|b)=\frac{P(b|a)P(a)}{P(b)}$

in distribution form $P(Y|X)=\alpha P(X|Y)P(Y)$

Useful for assessing diagnostic probability from causal probability.

$P(\text{Cause}|\text{Effect})=\frac{P(\text{Effect}|\text{Cause})P(\text{Cause})}{P(\text{Effect})}$

This is a typical ML problem!